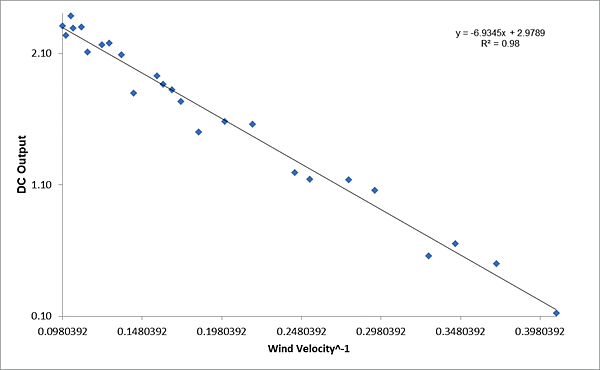
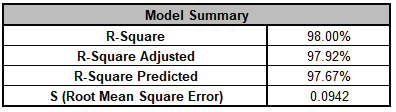
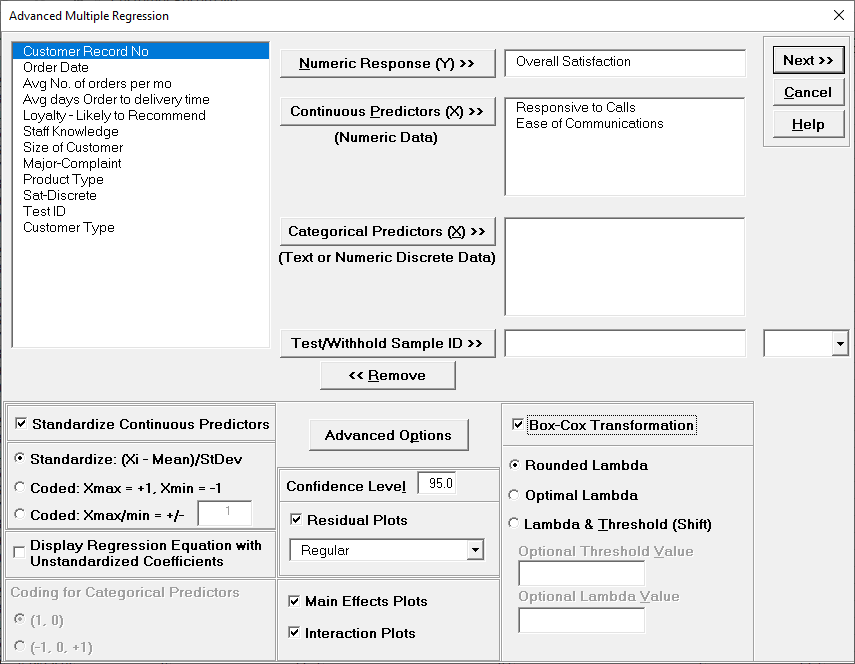
Advanced Multiple Regression
- Home /
- Fit Multiple Regression Model
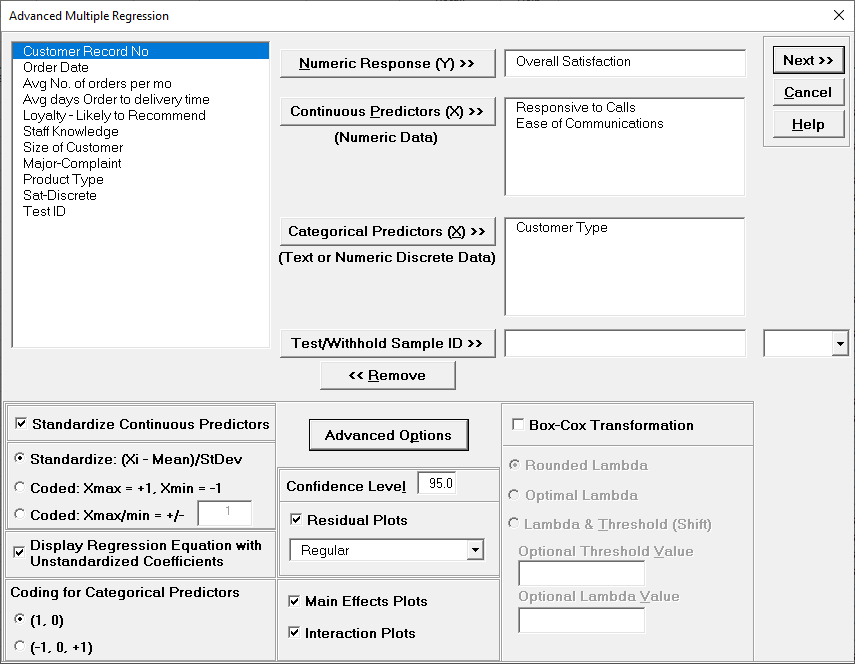
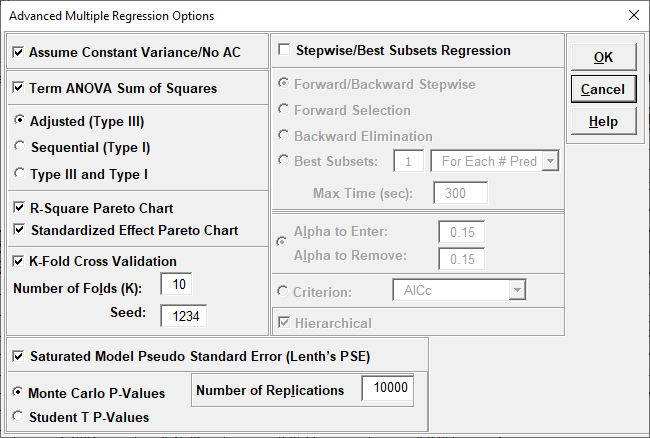
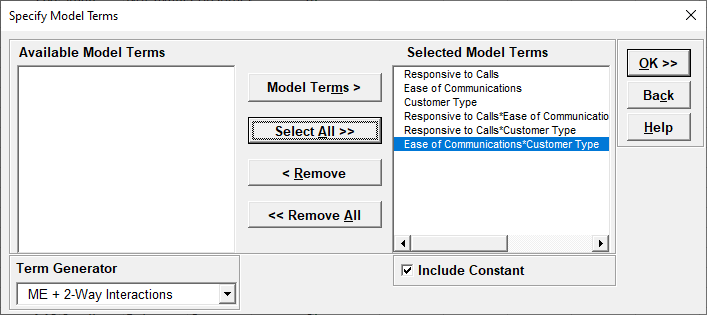
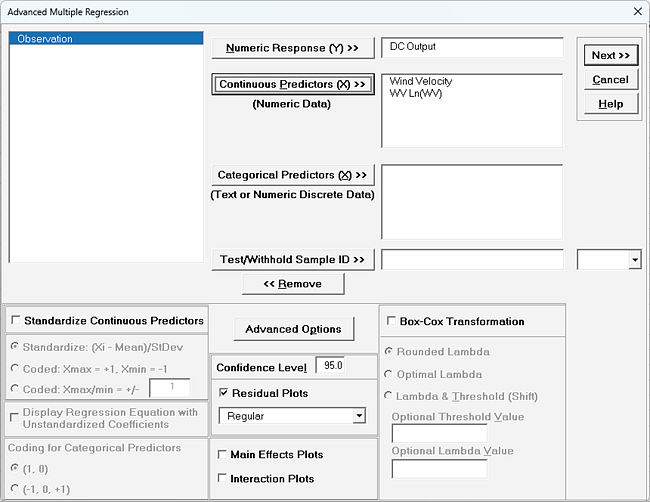
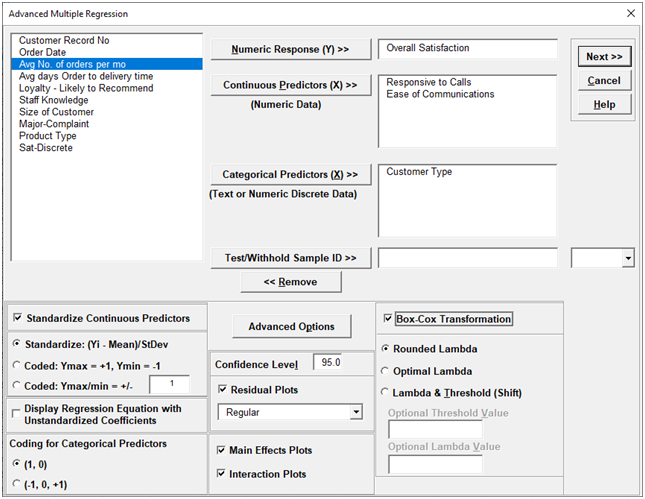
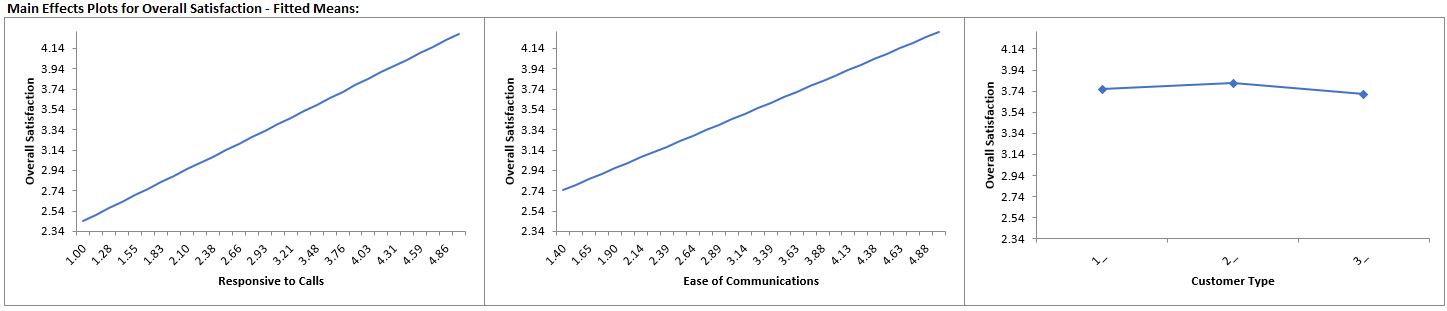
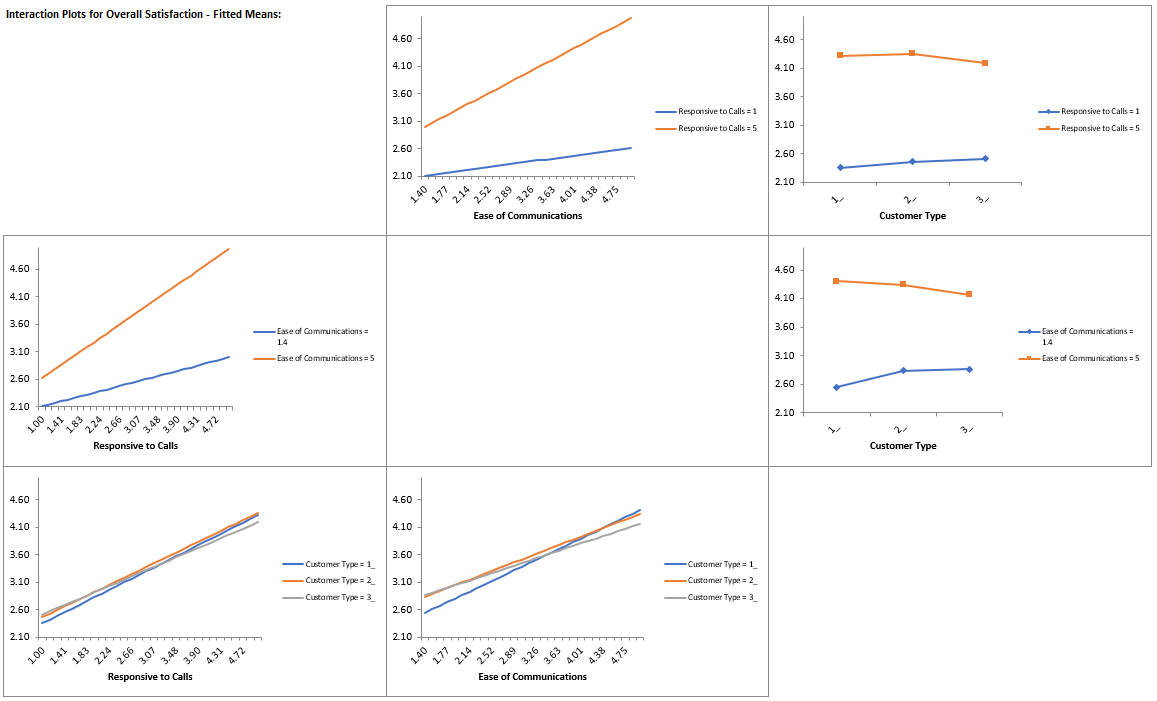
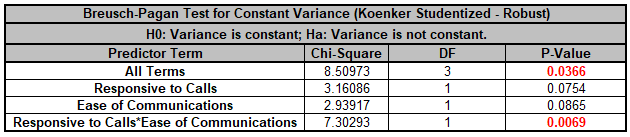
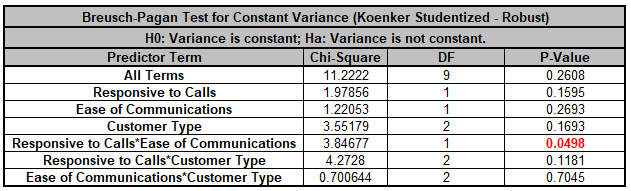
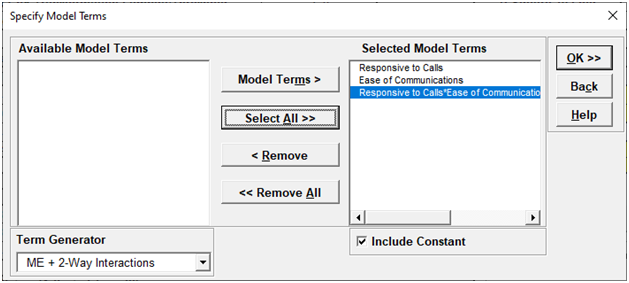
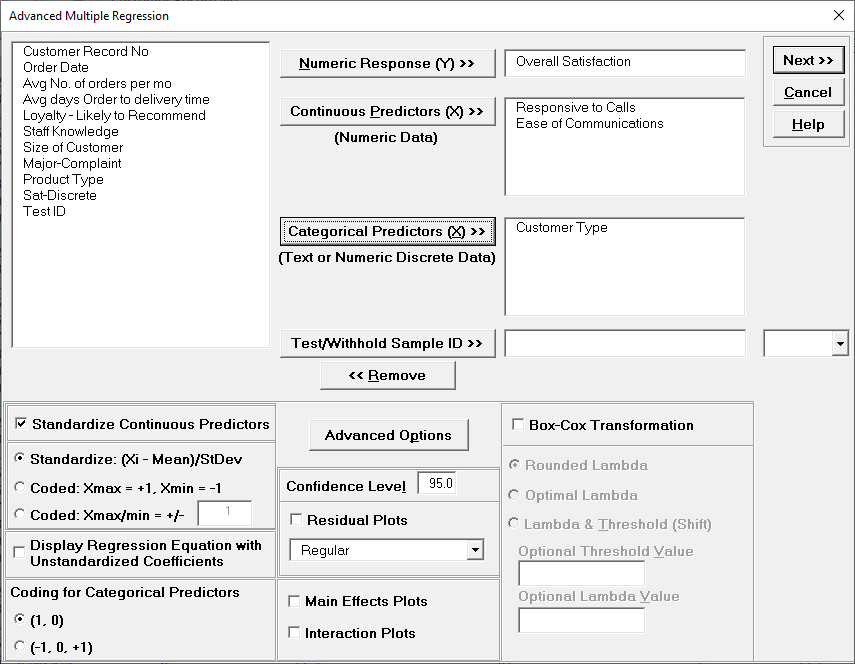
We are adding the three possible 2-way interactions. Note that the three interaction terms are: continuous*continuous, continuous*categorical and continuous*categorical.
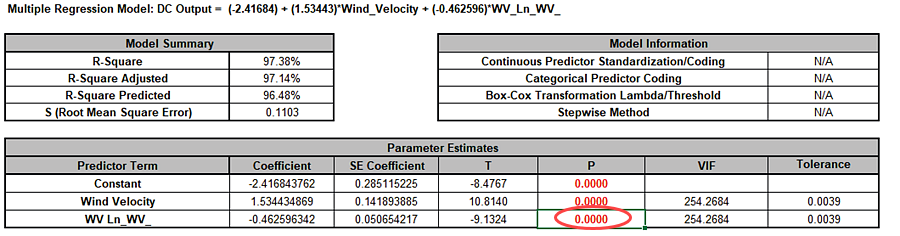
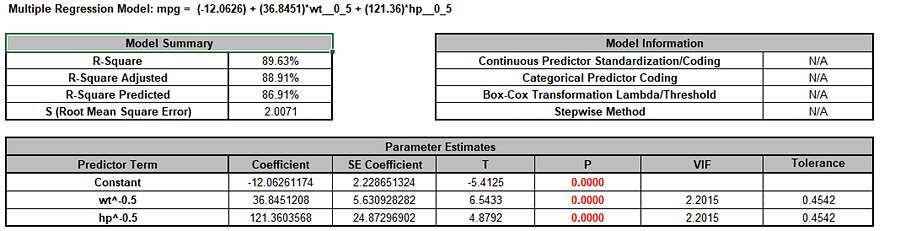
Multiple Regression Model (Uncoded): Overall Satisfaction = (1.38507)
+ (0.111481)*Responsive_to_Calls
+ (0.126645)*Ease_of_Communications
+ (0.505067)*(IF(Customer_Type="2_",1,0))
+ (0.821635)*(IF(Customer_Type="3_",1,0))
+ (0.101385)*Responsive_to_Calls*Ease_of_Communications
+ (-0.0184748)*Responsive_to_Calls*(IF(Customer_Type="2_",1,0))
+ (-0.0728492)*Responsive_to_Calls*(IF(Customer_Type="3_",1,0))
+ (-0.0997064)*Ease_of_Communications*(IF(Customer_Type="2_",1,0))
+ (-0.156844)*Ease_of_Communications*(IF(Customer_Type="3_",1,0))
Note blanks and special characters in the predictor names are converted to the underscore character "_". The numeric Customer Type 1, 2, 3 has also been converted to text so appears as "1_", "2_", "3_", where "1_" is the hidden reference level.
For categorical predictors, IF statements are used, but exclude the hidden reference level.
This is the display version of the prediction equation given at cell L14 (which has more precision for the coefficients and predictor names are converted to legal Excel range names by padding with the underscore "_" character). If the equation exceeds 8000 characters (Excel's legal limit for a formula is 8192), then a truncated version is displayed and cell L14 does not show the formula.
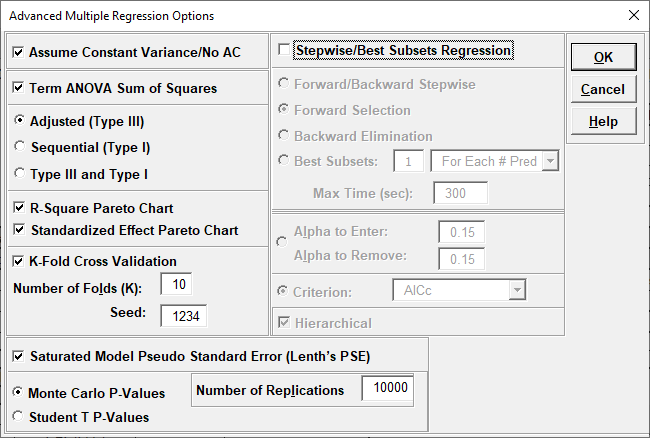
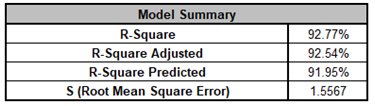
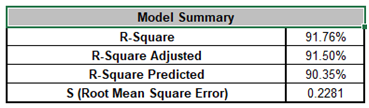
Note, these coefficients do not match those given in the Parameter Estimates table, since they are Standardized. If consistency is desired, one can always rerun the analysis with Display Regression Equation with Unstandardized Coefficients unchecked.
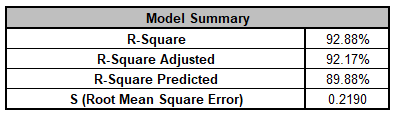

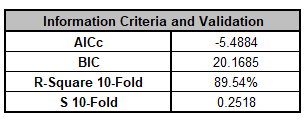
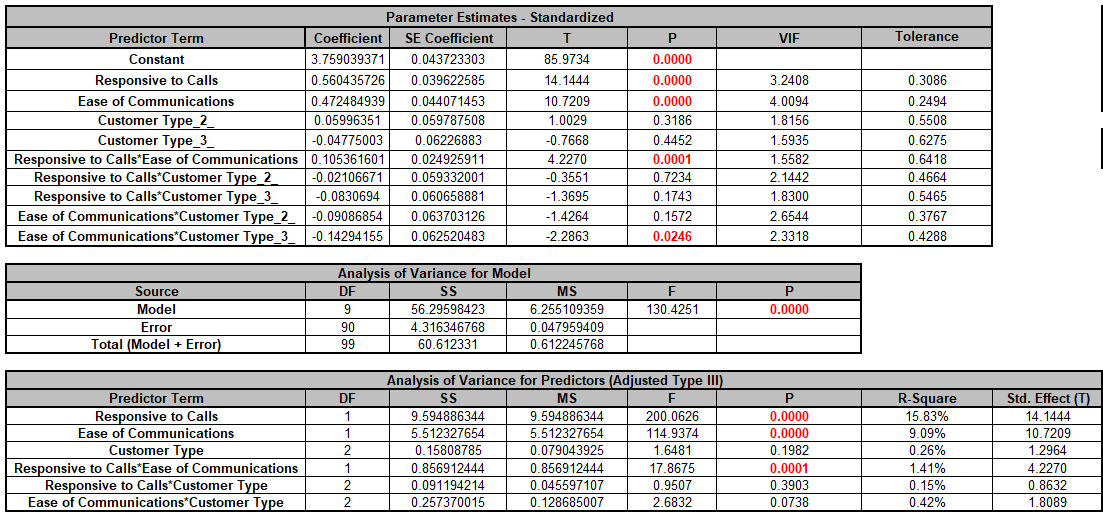
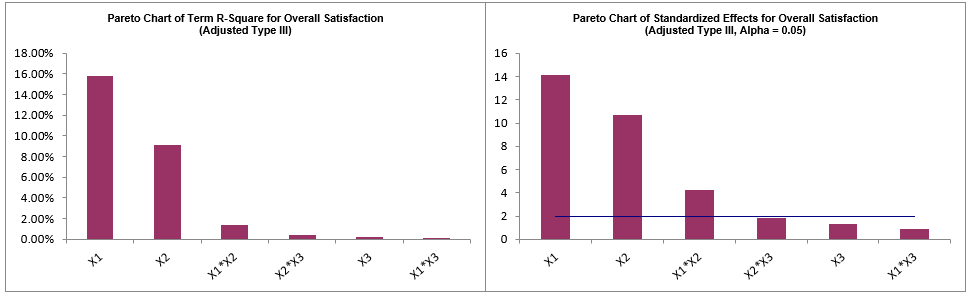

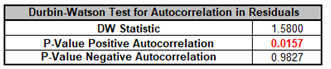
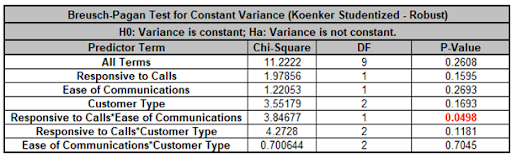

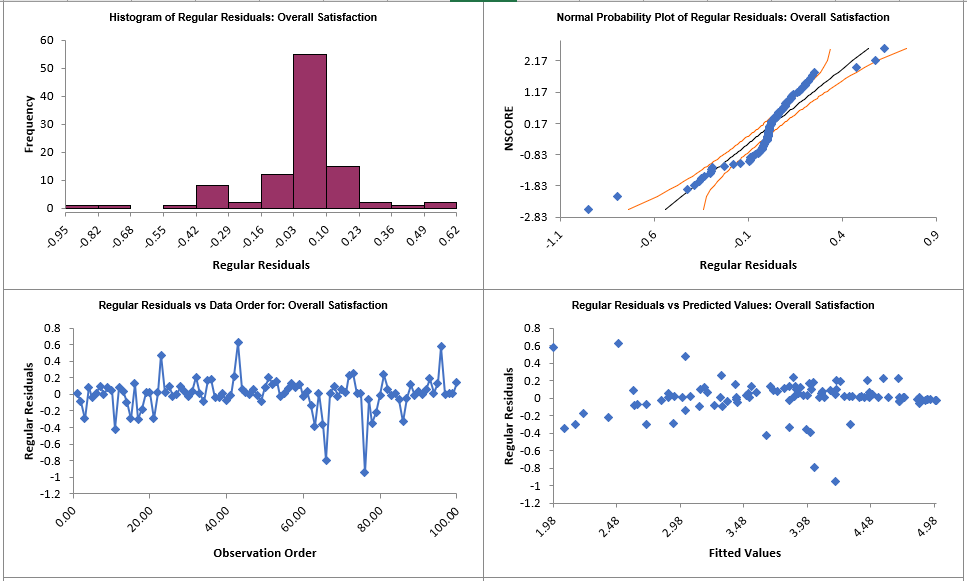
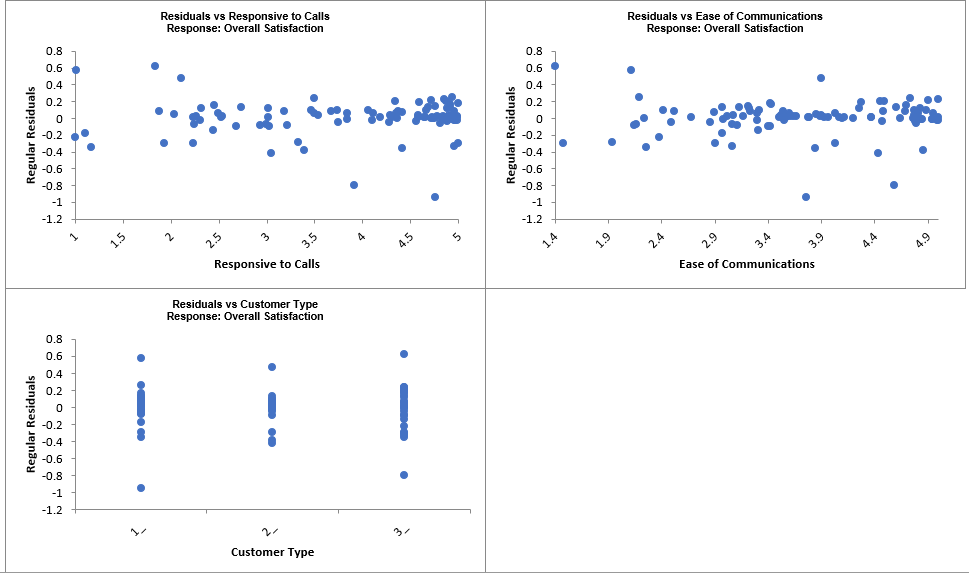







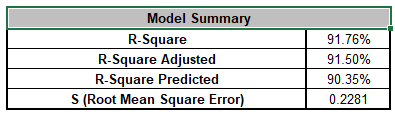

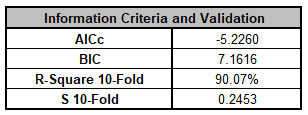
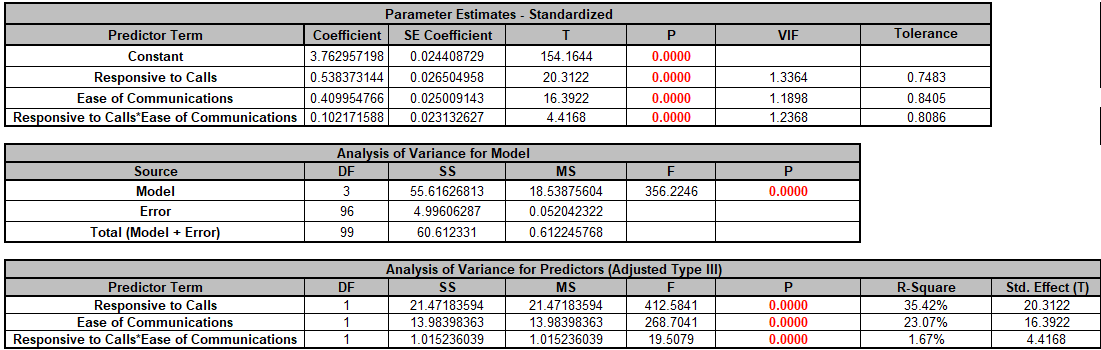
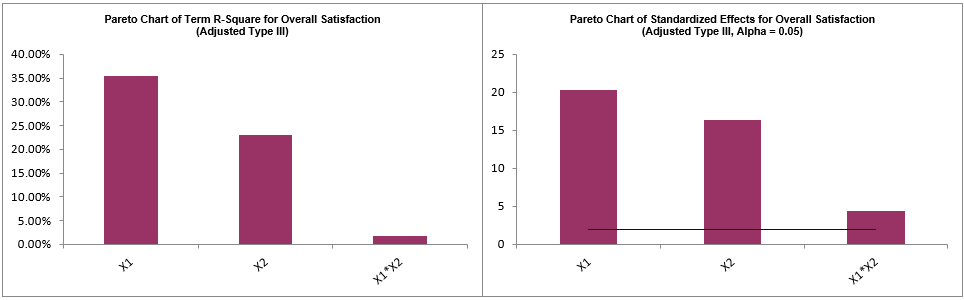




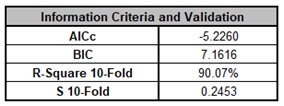
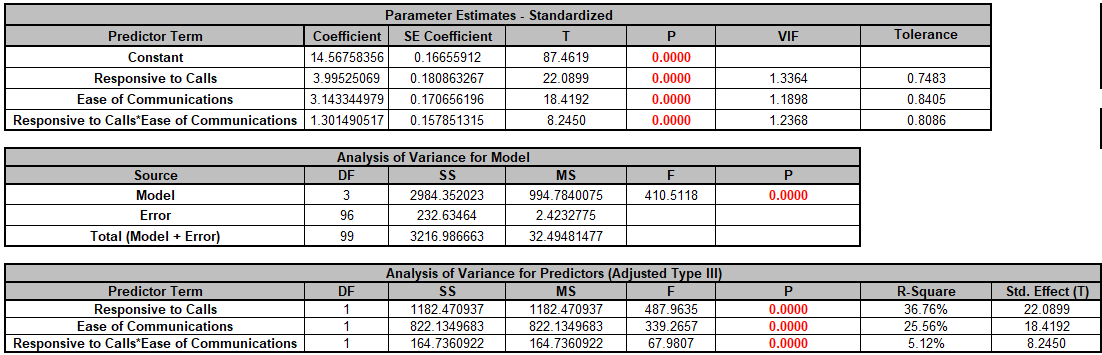
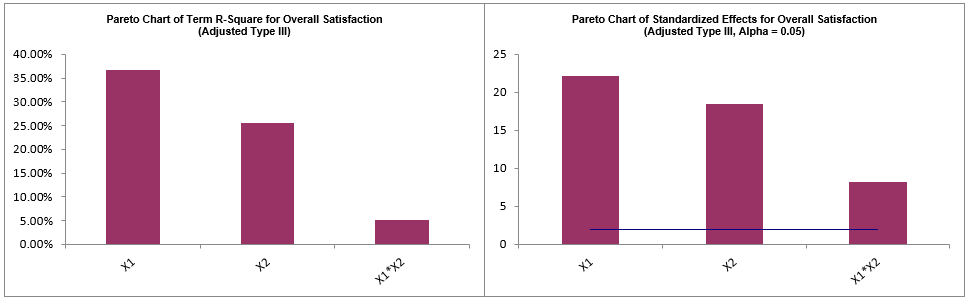

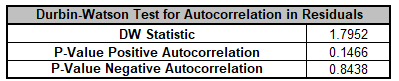
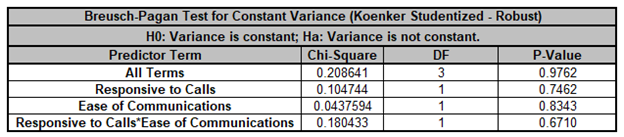
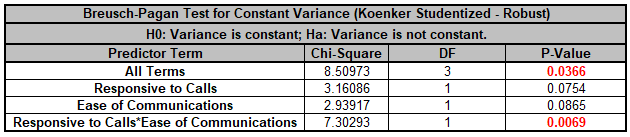
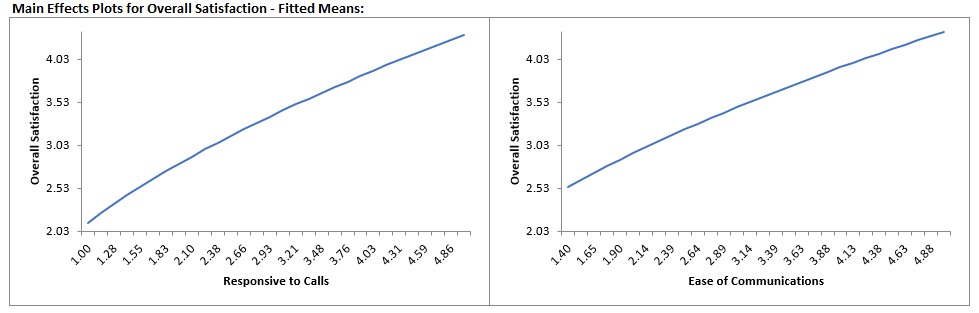
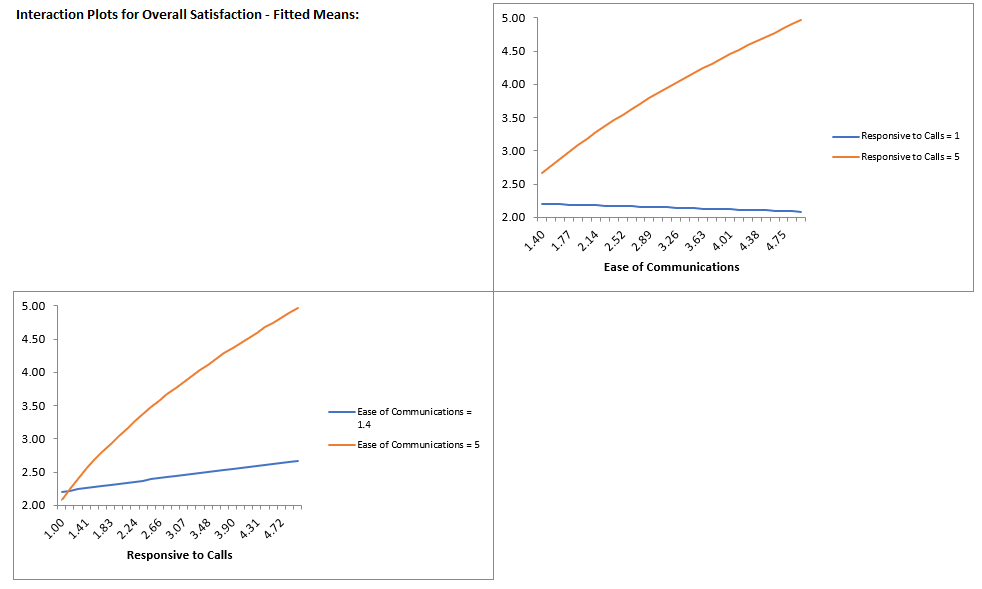


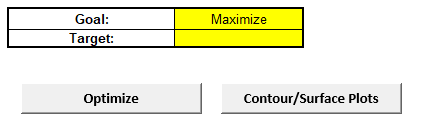
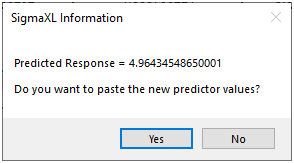

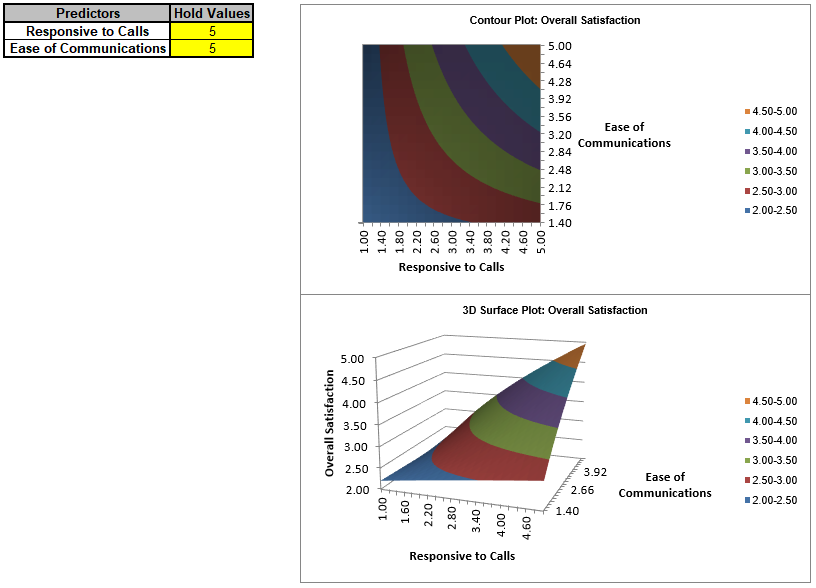
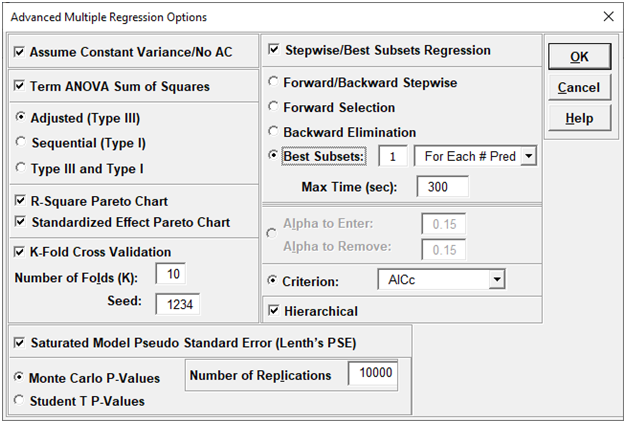
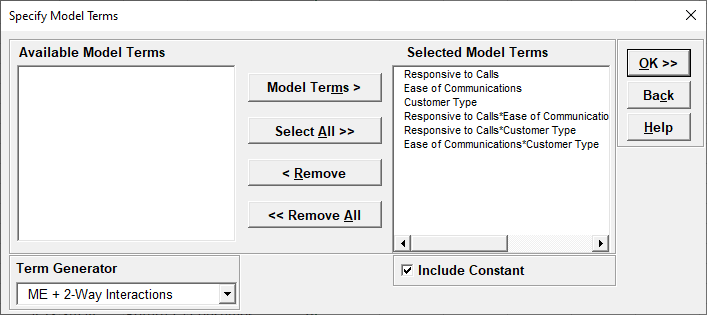



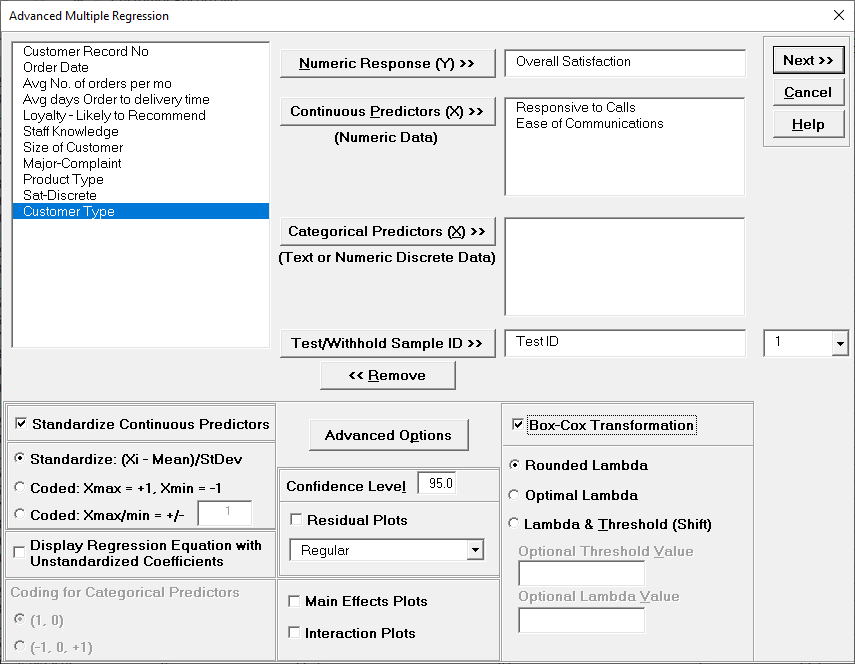
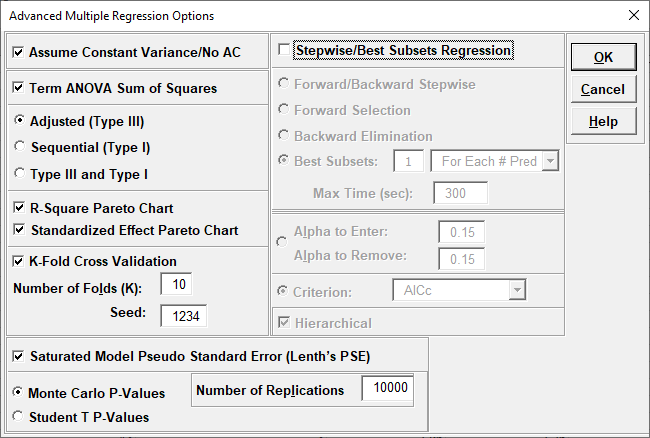



For details, see the Appendix: Advanced Multiple Regression. Note, in SigmaXL: