How Do I Perform Multiple Regression in Excel Using SigmaXL?
Multiple Regression analyzes the relationship between one dependent variable (Y) and multiple independent variables (X's). It is used to discover the relationship between the variables and create an empirical equation of the form:Y = b0 + b1*X1 + b2*X2 + ... + bn*Xn
This equation can be used to predict a Y value for a given set of input X values. SigmaXL uses the method of least squares to solve for the model coefficients and constant term. Statistical tests of hypothesis are provided for the model coefficients.
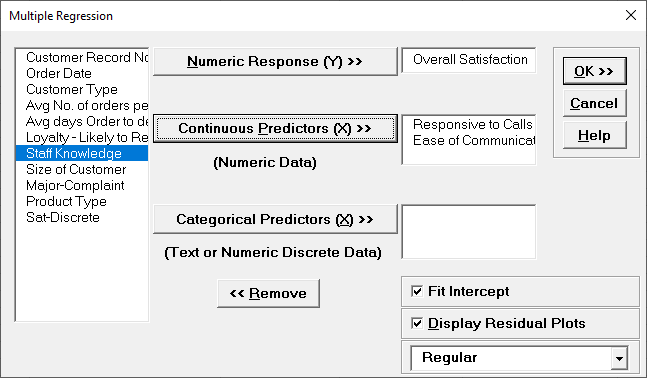
- Open Customer Data.xlsx. Click Sheet 1 Tab. Click SigmaXL > Statistical Tools > Regression > Multiple Regression. If necessary, click Use Entire Data Table, click Next.
- Select Overall Satisfaction, click Numeric Response (Y) >>, select
Responsive to Calls and Ease of Communications, click Continuous Predictors (X) >>.
Fit Intercept is checked by default. Check Display Residual Plots as shown:
- Click OK. The resulting
Multiple Regression report is shown:
- The variance inflation factor (VIF) and Tolerance scores are used to measure multicollinearity or correlation among predictors. VIF = 1 indicates no relation among predictors (which is highly desirable – you will see examples of this in Design of Experiments); VIF > 1 indicates that the predictors are correlated; VIF > 5 indicates that the regression coefficients are strongly correlated and this will lead to poor estimates of the coefficients. Tolerance = 1/VIF.
- The Durbin-Watson Test is used to determine if the residuals are autocorrelated. If either p-value is < .05, then there is significant autocorrelation. This is likely due to an external bias factor affecting your process over time (e.g. “warm-up” effect, seasonality). This will also be evident in the plot of residuals versus observation order. Autocorrelation in the residuals is not a problem for this model.
- If the Fit Intercept option is unchecked, the following diagnostics are not reported due to statistical issues associated with the removal of the constant. These are: R-Square, R-Square Adjusted, VIF (Variance Inflation Factor) and Tolerance collinearity diagnostics, DW (Durbin-Watson) autocorrelation report, Anova report for Discrete factors (discrete factors will not be permitted when "Fit Intercept" is unchecked). All other tests including residual diagnostics are reported. Users can run the model with the "Fit Intercept" on to get the above statistics and then run with "Fit Intercept" off.
- A predicted response calculator allows you to enter X values and obtain the predicted response value, including the 95% confidence interval for the long term mean and 95% prediction interval for individual values:
- Click the Mult Reg Residuals Sheet and scroll right to view the Residual Plots shown below:
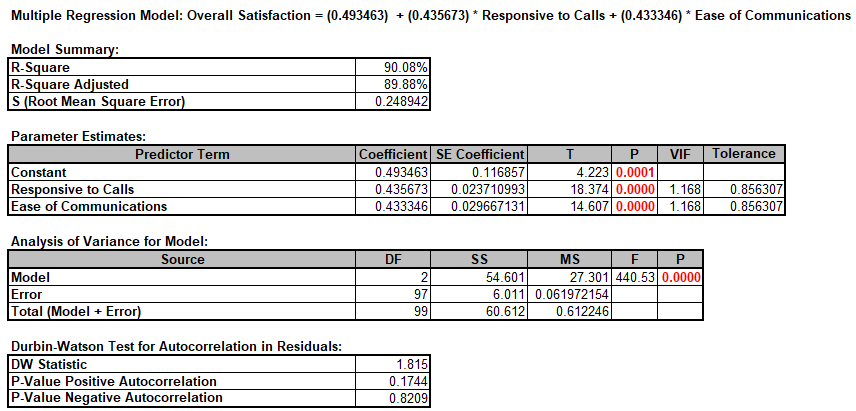
This model of Overall Satisfaction as a function of Responsiveness to Calls and Ease of Communications looks very good with an R-Square value of 90%. Both Predictors are shown to be significant with their respective p-values < .05. Clearly we need to focus on these two X factors to improve customer satisfaction.

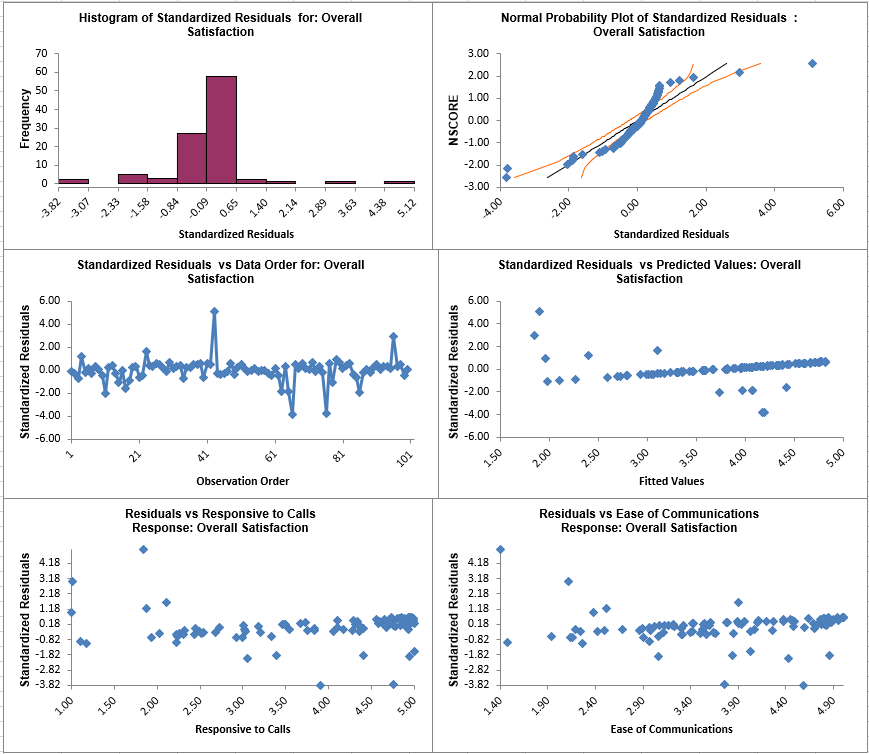
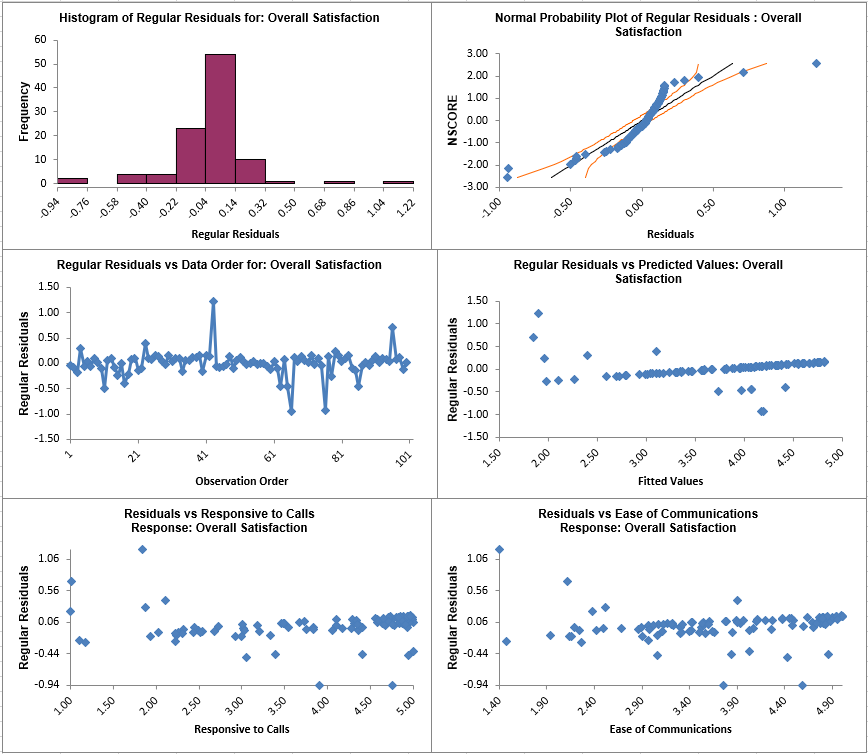 Residuals are the unexplained variation from the regression model (Y - Ŷ). We expect to see the residuals normally distributed with no obvious patterns in the above graphs. Clearly this is not the case here, with the
Residuals versus Predicted Values indicating there is likely some other X factor influencing the Overall Satisfaction. It would be appropriate to consider other factors in the model.
Residuals are the unexplained variation from the regression model (Y - Ŷ). We expect to see the residuals normally distributed with no obvious patterns in the above graphs. Clearly this is not the case here, with the
Residuals versus Predicted Values indicating there is likely some other X factor influencing the Overall Satisfaction. It would be appropriate to consider other factors in the model. - SigmaXL also provides Standardized Residuals and Studentized (Deleted t) Residuals. The standardized residual is the residual, divided by an estimate of its standard deviation. This makes it easier to detect outliers. Standardized residuals greater than 3 and less than -3 are considered large (these outliers are highlighted in red). Studentized deleted residuals are computed in the same way that standardized residuals are computed, except that the ith observation is removed before performing the regression fit. This prevents the ith observation from influencing the regression model, resulting in unusual observations being more likely to stand out.
- Click Recall Last Dialog (or press F3). Change the
Residual type to Standardized. Click
OK. The resulting Standardized Residual plots are displayed:
- Other diagnostic measures reported but not plotted include Leverage, Cook's Distance (Influence), and DFITS. Leverage is a measure of how far an individual X predictor value deviates from its mean. High leverage points can potentially have a strong effect on the estimate of regression coefficients. Leverage values fall between 0 and 1. Cook's distance and DFITS are overall measures of influence. An observation is said to be influential if removing the observation substantially changes the estimate of coefficients. Cook’s distance can be thought of as the product of leverage and the standardized residual; DFITS as the product of leverage and the studentized residual.
- The easiest way to identify observations with high leverage and/or influence is to plot the measures on a run chart.
Multiple Regression with Continuous and Categorical Predictors
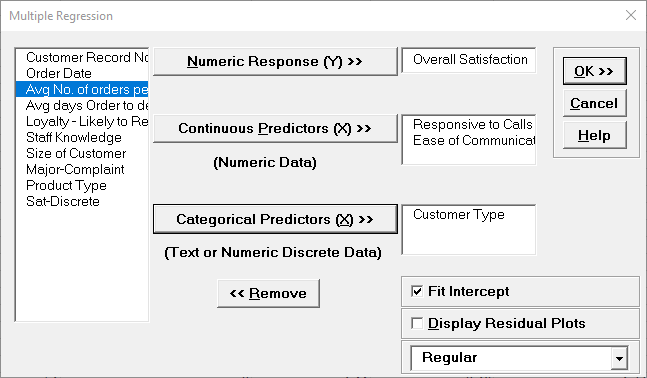
- Click Recall Last Dialog (or press F3). Select Customer Type, click Categorical Predictor (X) >>. We will not discuss residuals further so you may wish to uncheck Display Residual Plots. Keep Overall Satisfaction as the Numeric Response (Y) and Responsive to Calls and Ease of Communications as the Continuous Predictors (X):
- Click OK. The resulting Multiple Regression report is shown:
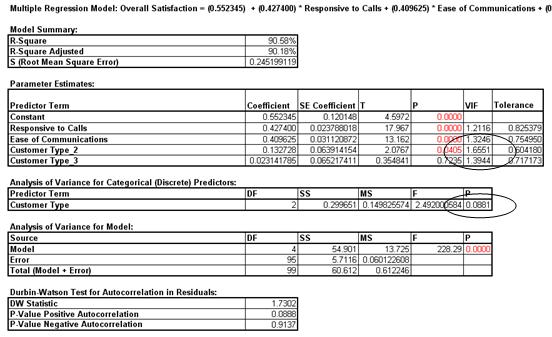
- The parameter estimates table now includes Customer Type 2 and Customer Type 3, but where is Customer Type 1? Since Customer Type is a discrete predictor, SigmaXL applies “dummy coding” (i.e. Customer Type 1 corresponds to Coded Variable 1 = 0 and Coded Variable 2 = 0; Customer Type 2 has Coded Variable 1 = 1 and Coded Variable 2 = 0; and Customer Type 3 has Coded Variable 1 = 0 and Coded Variable 2=1). Hence Customer Type 1 becomes the “hidden” or reference value. Other statistical software packages may use a different coding scheme based on -1,0,+1 instead of 0,1. The advantage of a 0,1 coding scheme is the relative ease of interpretation when making predictions with the model.
- In the Predicted Response Calculator enter the settings as shown:
- Note the addition of the Analysis of Variance for Categorical (Discrete) Predictors. The Customer Type p-value is .08, so we do not have strong evidence to keep this term in the model. However, many practitioners will use an alpha value of 0.1 as a criterion for removal. You are probably wondering why the p-value for Customer Type is not lower given the results we saw earlier using ANOVA. The change in p-value is due to the inclusion of Responsive to Calls and Ease of Communications in the model. We have higher scores for Ease of Communications and Responsive to Calls with Customer Type 2. Statistically, Customer Type is somewhat correlated to Responsive to Calls and Ease of Communications (VIF for Customer Type = 1.66 and 1.39).

Note that for Customer Type 1, you would enter Customer Type 2 = 0 and Customer Type 3 = 0; for Customer Type 2, as shown, you entered Customer Type 2 = 1 and Customer Type 3 = 0; for Customer Type 3 you would enter Customer Type 2 = 0 and Customer Type 3 = 1.
Web Demos
Our CTO and Co-Founder, John Noguera, regularly hosts free Web Demos featuring SigmaXL and DiscoverSim
Click here to view some now!
Contact Us
Phone: 1.888.SigmaXL (744.6295)
Support: Support@SigmaXL.com
Sales: Sales@SigmaXL.com
Information: Information@SigmaXL.com