Chi-Square Test – Fisher’s Exact

The Chi-Square Test – Fisher’s Exact utilizes permutations and fast network algorithms to solve the Exact Fisher P-Value for contingency (two-way row*column) tables. This is an extension of the Fisher Exact option provided in the Two Proportion Test template. For data that requires more computation time than specified, Monte Carlo P-Values provide an approximate (but unbiased) P-Value that typically matches exact to two decimal places using 10,000 replications. One million replications give a P-Value that is typically accurate to three decimal places. A confidence interval (99% default) is given for the Monte Carlo P-Values. For further details refer to the Appendix: Exact and Monte Carlo P-Values for Nonparametric and Contingency Tests.

It is important to note that while exact P-Values are “correct,” they do not increase (or decrease) the power of a small sample test, so they are not a solution to the problem of failure to detect a change due to inadequate sample size!

1. We will now re-analyze the data from the Chi-Square Test & Association example for Major Complaint by Customer Type. Open Customer Data.xlsx. Click Sheet 1 tab. The discrete data of interest is Complaints and Customer Type, i.e., does the type of complaint differ across customer type? Formally the Null Hypothesis is that there is no relationship (or independence) between Customer Type and Complaints.


2. Click SigmaXL > Statistical Tools > Chi-Square Tests – Exact > Chi-Square Test – Fisher’s Exact. Ensure that the entire data table is selected. If not, check Use Entire Data Table. Click Next.


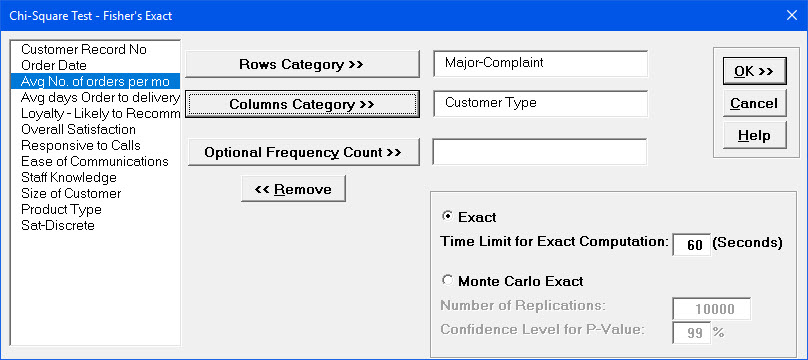
3. Select Major-Complaint, click Count Category (X1) >>; select Customer Type, click Group Category (X2) >>. Select Exact with the default Time Limit for Exact Computation = 60 seconds.
   
   
   
   Tip: If the exact computation time limit is exceeded a dialog will prompt you to use Monte Carlo or to increase the computation time. When this occurs, Monte Carlo is recommended.


4. Click OK. Results:
   
   
   
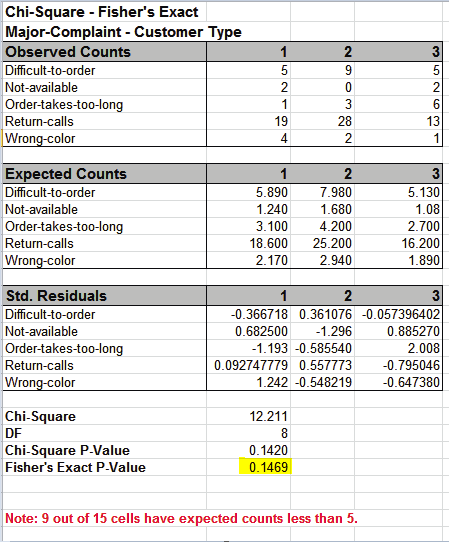
   With Fisher’s Exact P-Value = 0.1469 we fail to reject H0, so we cannot conclude that there is a difference in customer complaints across customer types. This is close to the approximate Chi-Square P-Value of 0.142, so either P-Value results in the same conclusion.
   
   However, there are cases where the “large sample” Chi-Square P-Value leads to one conclusion but Fisher’s Exact P-Value gives another. This will be demonstrated later using Two Way Table Data – Fisher’s Exact.
   
   The Exact P-Value was computed very quickly, but if the data set was larger, the required computation time could become excessive, and Monte Carlo would be required. We will rerun this analysis with Monte Carlo and discuss the output report.


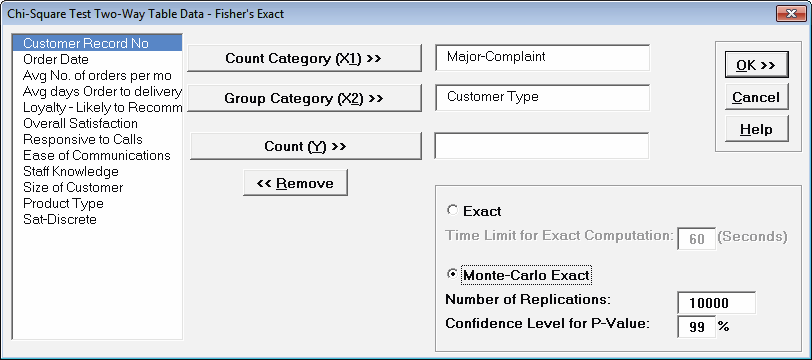
5. Press F3 or click Recall SigmaXL Dialog to recall last dialog. Select Monte Carlo Exact with the default Number of Replications = 10000 and Confidence Level for P-Value = 99%.
   
   
   
   Tip: As discussed above 10,000 replications will result in a Monte Carlo P-Value that is correct to two decimal places. One million (1e6) replications will result in three decimal places of accuracy and typically require less than 60 seconds to solve for any data set.
   
   Tip: The Monte Carlo 99% confidence interval for P-Value is not the same as a confidence interval on the test statistic due to data sampling error. The confidence level for the hypothesis test statistic is still 95%, so all reported P-Values less than .05 will be highlighted in red to indicate significance. The 99% Monte Carlo P-Value confidence interval is due to the uncertainty in Monte Carlo sampling, and it becomes smaller as the number of replications increases (irrespective of the data sample size). The Exact P-Value will lie within the stated Monte Carlo confidence interval 99% of the time.


6. Click OK. Results:
   
   
   
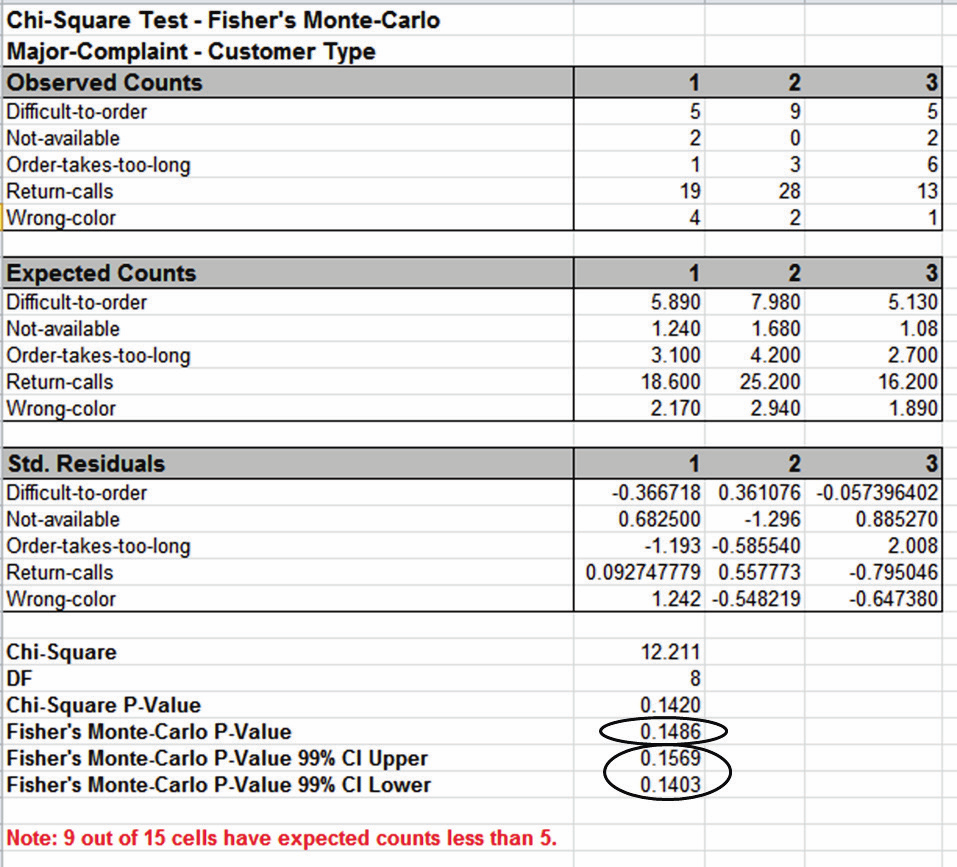
   Fisher’s Monte Carlo P-Value here is 0.1486 with a 99% confidence interval of 0.1403 to 0.1569. This will be slightly different every time it is run (the Monte Carlo seed value is derived from the system clock). The true Exact P-Value = 0.1469 lies within this confidence interval. If the confidence interval is too wide (e.g., upper “fail-to-reject” H0 and lower “reject” H0), simply rerun the Monte Carlo option using a larger number of replications (use 1e5 or 1e6).