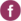Advanced Design of Experiments: Optimal Designs Dialog

SigmaXL > Design of Experiments > Advanced Design of Experiments: Optimal > Optimal Designs

1. Optimal design of experiments is a method for planning experiments to maximize the amount of information gained while using the fewest resources. The design of experiments is undertaken by an iterative search algorithm that seeks to optimize a design criterion for a given model with a specified number of runs. Linear constraints may be specified for the continuous factors. For formula and algorithm details, see the Appendix: Optimal Design. See also Example 6: Evaluating Optimal Designs and Example 7: Constrained D-Optimal Design - Adhesive Bond Strength.

2. Number of Continuous Factors - select 0 to 19 continuous factors. Modify Factor Names and Level Settings (Continuous) as needed. Name is text , Low and High settings are numeric .

3. Number of Categorical Factors - select 0 to 10 categorical factors. Modify Factor Names and Level Settings (Categorical) as needed. Name is text , No. Levels can be 2 to 10, Level Values are text. The categorical factor coding scheme is (-1,0,1).

4. The minimum number of continuous factors + categorical factors = 1. The maximum number = 19.

5. Number of Blocks - select from 1 to 100.

6. The Number of Additional Runs/Points for Model specify the number of runs in addition to the minimum required by the model (i.e., number of coefficient terms including constant). The default value is 6. If 0 is specified (with h Minimum Number of Replicate Runs/Points = 0 and Minimum Number of Center Points for Continuous = 0) , the error df will be 0; the recommended minimum additional runs is 3.

7. If Minimum Number of Replicate Runs/Points > 0 or Minimum Number of Center Points for Continuous > 0, a constraint is added to the objective function to ensure that these requirements are met. Note that if Minimum Number of Center Points for Continuous > 0 and there are categorical factors, the categorical factor levels will not necessarily be balanced.

8. Select Design Criterion: D-Optimality to specify a D-Optimal design that maximizes the determinant of the XX'XX information matrix, which minimizes the volume of the joint confidence region of the estimated regression coefficients. This results in good overall model precision, so is recommended as a general purpose alternative to screening and two-level factorial designs.

9. Select Design Criterion: I-Optimality to specify a I-Optimal design that minimizes the trace of (XX'XX)-1MM, where MM is the moment matrix for the given model. This minimizes the average prediction variance (integrated variance) over the design space, which can be thought of as minimizing the area under the Fraction of Design Space (FDS) Plot. Since the primary objective of a Response Surface design is accurate prediction and optimization, I-Optimality is recommended for RSM designs. Note that currently I-Optimal is not available if there are linear constraints.

10. Select Design Criterion: A-Optimality to specify a A-Optimal design that minimizes the trace of (XX'XX)-1, which minimizes the average variance of the estimated regression coefficient terms and is recommended for screening designs.

11. Check Continuous Linear Constraints to specify constraints and enter formula(s) with uncoded/actual values, separated by a semicolon ';'. Use factor letters (A to T, excluding I) as a shorthand notation or factor names. Example: A + 2*B >= 0.5; A + 2*B <= 1.75. If factor letters are used, the constraint formula will be displayed using the factor names.

12. Constraint formulas apply only to continuous factors and must be linear. Use comparison operators '>=' or '<=' to define constraints. The formula must be on the left-hand side and the numeric value on the right-hand side. Illegal constraint formulas are error trapped. Note, factor levels can be any continuous value within the constraint region

13. Note that for analysis, constraint formulas will automatically be applied to Optimize and Multiple Response Optimization, but not to Contour and Surface Plots

14. Tip: SigmaXL does not directly support Mixture designs, but they can be created using a Slack Variable model, where one of the mixture variables is removed from the design model and the constraint formula. For example, the mixture constraint A + B + C = 1 with Low = 0 and High = 1 for each factor and factor A designated as the slack variable, would be written as:

    1. B + C >= 1 - A(High)
    2. B + C <= 1 - A(Low)
    With the final constraint formulas specified as
    3. B + C >= 0; B + C <= 1
    Additional constraints may be specified. Note, the analysis of the mixture design must also exclude the slack variable.

15. The MIDACO settings of Maximum Time (seconds) and Maximum Function Evaluations with no Change (x1000) may be modified. The default settings are 300 seconds and 100,000 function evaluations, but 600 seconds and 1,000,000 evaluations may be needed for a complex problem with more than 30 terms, includes multi-level categorical terms or constraints.

16. Randomize Runs - check to randomize runs with Seed (Base) as either Clock or specified Value The latter will randomize the runs but always in the same random order for the same seed value. If unchecked, runs are in given in standard order.

17. Fraction of Design Space (FDS) Plots. The FDS Plot uses the same model as specified for the Optimal design. For details on FDS Plots see the Appendix: : Fraction of Design Space (FDS) Plots. Example 5: Evaluating Response Surface Designs with the Fraction of Design Space (FDS) Plot. See also Example 5: Evaluating Response Surface Designs with the Fraction of Design Space (FDS) Plot.

18. Number of Responses - specify number of responses and enter Response Name.

19. After specifying a model, the Total No. of Runs = Number of runs required by the model + Number of Additional Runs/Points for Model + Minimum Number of Replicate Runs/Points + Minimum Number of Center Points for Continuous.