Kruskal-Wallis – Exact

This tool is used to estimate the exact P-Value using Monte Carlo. Typically this would not be necessary unless the sample sizes were smaller (each sample N <= 5 for Kruskal-Wallis), but this gives continuity on the example.

Computing an exact P-Value for Kruskal-Wallis is very computationally intensive. The Network Model by Mehta and Patel cannot be used for this test (see Appendix Exact and Monte Carlo P-Values for Nonparametric and Contingency Tests). In this example, the total number of permutations are:

(31+42+27)! / (31! * 42! * 27!) = 7.42 E44

(i.e., more than the number of stars in the observable universe). So we will not attempt to compute the exact, but rather use Monte Carlo.

1. Open Customer Data.xlsx, click on Sheet 1 tab (or press F4 to activate last worksheet).


2. Click SigmaXL > Statistical Tools > Nonparametric Tests - Exact > Kruskal-Wallis - Exact. If necessary, check Use Entire Data Table, click Next.


3. Ensure that Stacked Column Format is checked. Select Overall Satisfaction, click Numeric Data Variable (Y) >>; select Customer Type, click Group Category (X) >>. Select Monte Carlo Exact with the Number of Replications = 1e6 and Confidence Level for P-Value = 99%. One million replications are used because the expected P-Value is very small as estimated from the “large sample” Kruskal-Wallis above. This will take up to a minute to run, so if you have a slow computer, use 1e5 replications instead of 1e6.
   
   
   
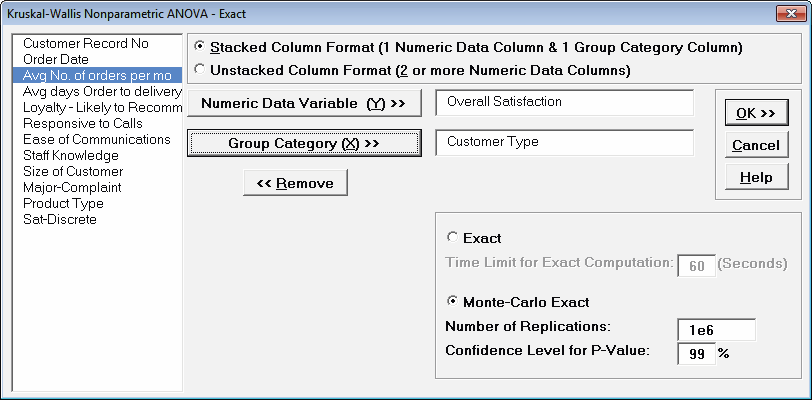
   Tip: The Monte Carlo 99% confidence interval for P-Value is not the same as a confidence interval on the test statistic due to data sampling error. The confidence level for the hypothesis test statistic is still 95%, so all reported P-Values less than .05 will be highlighted in red to indicate significance. The 99% Monte Carlo P-Value confidence interval is due to the uncertainty in Monte Carlo sampling, and it becomes smaller as the number of replications increases (irrespective of the data sample size). The Exact P-Value will lie within the stated Monte Carlo confidence interval 99% of the time.


4. Click OK.
   
   
   
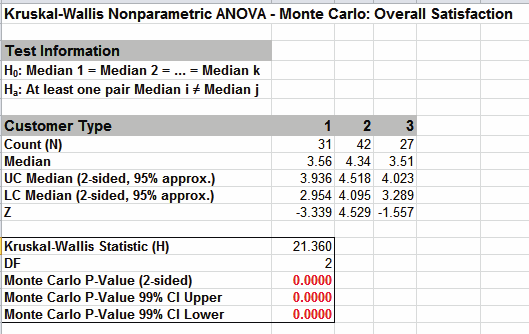
   Click on cell B16 to view the P-Value with more decimal place precision (or change the cell format to scientific notation). The Monte Carlo P-Value here is 0.000009 (9 e-6) with a 99% confidence interval of .000002 (2 e-6) to 0.000016 (1.6 e-5). This will be slightly different every time it is run (the Monte Carlo seed value is derived from the system clock). So we reject H0: at least one pairwise set of medians are not equal.
   
   Note that the large sample (asymptotic) P-Value of 2.3 e-5 lies outside of the Monte Carlo exact confidence interval.
   
   
5. Now we will consider a small sample problem. Open Snore Study.xlsx. This data is from:
   
   Gibbons, J.D. and Chakraborti, S. (2010). Nonparametric Statistical Inference (5th Edition). New York: Chapman & Hall, (Example 10.2.1 data, page 347; Example 10.4.2 analysis, pp. 360 – 362).
   
   An experiment was conducted to determine which device is the most effective in stopping snoring or at least in reducing it. Fifteen men who are habitual snorers were divided randomly into three groups to test the devices. Each man’s sleep was monitored for one night by a machine that measures the amount of snoring on a 100-point scale while using a device.


6. Select Snore Study Data tab. Click SigmaXL > Statistical Tools > Nonparametric Tests – Exact > Kruskal-Wallis - Exact. If necessary, check Use Entire Data Table, click Next.


7. With Unstacked Column Format checked, select Device A, Device B and Device C, click Numeric Data Variables (Y) >>. Select Exact with the default Time Limit for Exact Computation = 60 seconds.
   
   


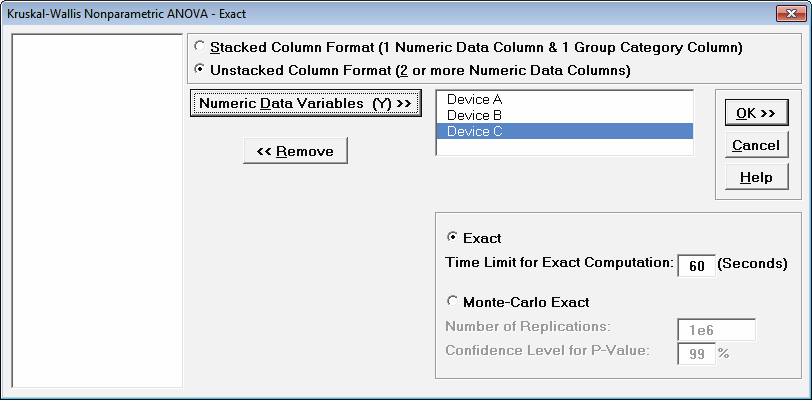
8. Click OK. Results:
   
   
   
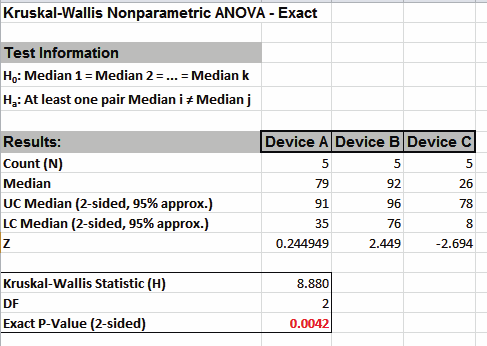
   With the Exact P-Value = 0.0042 we reject H0, and conclude that there is a significant difference in median snore study scores. This exact P-Value matches that given in the reference textbook using SAS and StatXact.
   
   By way of comparison, we will now rerun the analysis using the “large sample” or “asymptotic” Kruskal-Wallis test.


9. Select Snore Study Data tab (or press F4 to activate last worksheet). Click SigmaXL > Statistical Tools > Nonparametric Tests > Kruskal-Wallis. If necessary, check Use Entire Data Table, click Next.


10. With Unstacked Column Format checked, select Device A, Device B and Device C, click Numeric Data Variables (Y) >>.


11. Click OK. Results:
    
    
    
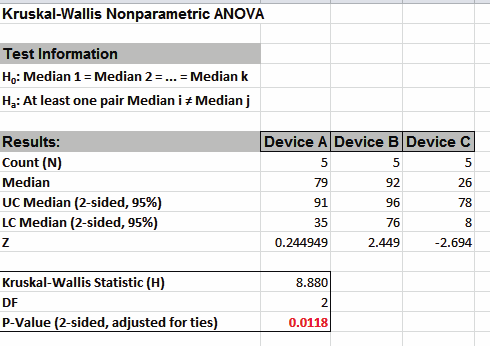
    With the P-Value = .0118 we reject H0 (using alpha = .05), but note that if we were using alpha = 0.01, we would have incorrectly failed to reject the null hypothesis. This “large sample” P-Value matches that given in the reference textbook using Minitab.
    
    In conclusion, whenever you have a small sample size and are performing a Nonparametric test, always use the Exact option.