Summary of Features in General Linear Model
Statistical Tools > General Linear Model > Fit General Linear Model
Extends Advanced Multiple Regression to include:
- Fixed and Random Factors
- Nested Factors
- Covariates (can be Nested)
- For Random or Mixed Random/Fixed Factors with a balanced design, the ANOVA and Variance Components (VC) report is given based on Expected Mean Squares. VC confidence intervals using Restricted Maximum Likelihood (REML) are included.
- If the design is unbalanced or model is non-hierarchical, REML is used to compute the VC values and confidence intervals. Fixed Effects Tests are based on Satterthwaite approximation degrees of freedom.
- Main Effects with Confidence Intervals and Interaction Plots of Fitted Means for Non-Nested Fixed Factors
- Tukey and Fisher Pairwise Comparison of Means for Non-Nested Fixed Factors
- Predicted Response Calculator
Statistical Tools > General Linear Model > GLM Multiple Response Optimization
- Multiple Response Optimization for Nested or Non-Nested Fixed Factors
For details on the statistical methods, formulas and references, see the Appendix: General Linear Model.
Multiple Response Optimization is introduced in Design of Experiments: Part F – Multiple Response Optimization with Advanced Multiple Regression.
Note that if a factor is nested in one model and used in another, it must be nested the same way for all models.
Case study examples using GLM will be used to demonstrate the analysis of:
- Fixed Factors with Nested Variable
- Sources of Variation Study
- Classical Gage R&R
- Gage R&R Study with Operator as Fixed Factor
- Destructive (Nested) Gage R&R
- Expanded Gage R&R
- Unbalanced Nested Factorial Experimentwith Fixed and Random Factors
For further reading, the following book is recommended:
Montgomery, D.C. (2020). Design and Analysis of Experiments, 10th Edition, John Wiley & Sons. See chapter 13 "Experiments with Random Factors" and chapter 14 "Nested and Split-Plot Designs".
General Linear Model Dialogs and Options
Fit General Linear Model Dialog
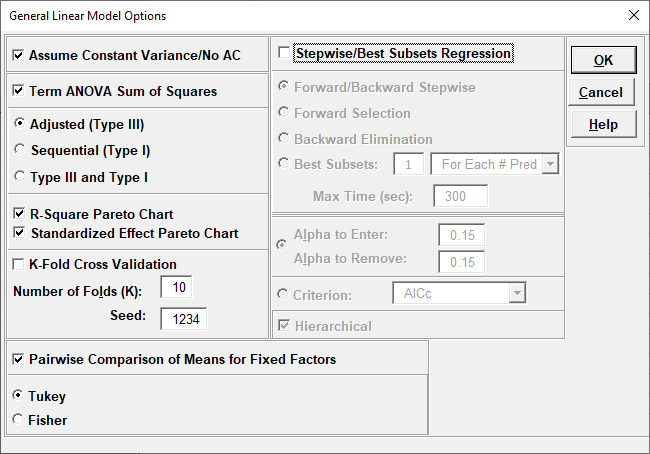
Tip: There are a lot of options here, giving the user flexibility for model refinement, but this can also be overwhelming to someone starting out with these tools. We recommend using the following settings for Stepwise/Best Subsets
Regression:
- Forward Selection, Criterion: AICc,
BIC or R-Square Predicted,
Hierarchical checked. This is fast and will build a model that minimizes
AICc, BIC or maximizes R-Square Predicted.
AICc or R-Square Predicted are recommended for the best model prediction accuracy,
BIC is recommended
for model parsimony. Note, however, this does not consider all possible models.
-
Best Subsets, 1 For Each # of Pred, Max Time (sec) = 300,
Criterion: AICc or BIC, Hierarchical checked. This can be slow but gives a very useful report of the best model for each number of predictors in the model.
Specify Model Terms Dialog
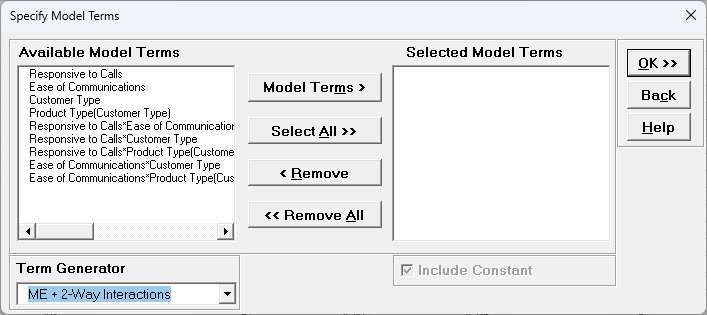
- Term Generator - select any of the following to build a list of
Available Model Terms:
- Main Effects - default - no change to original specified terms
- ME+ 2-Way Interactions - use this to include 2-way interactions in the model, for example, analyzing data from a Res IV or Res V fractional-factorial DOE. When specifying interactions or higher order terms, standardization
of continuous predictors is highly recommended.
- ME + 2-Way Interactions + Quadratic - use this to include 2-way interactions andquadratic terms in the model, for example, analyzing data from a response surface DOE. Categorical terms will not be squared.
- ME + All Interactions - use this to include all possible interaction terms in the model, for example analyzing data from a full-factorial DOE.
- All up to 3-Way - use this to include 2-way interactions, quadratic, 3-way interactions, quadratic*main effect and cubic terms in the model. Categorical terms will not be squared or cubed.
- Model Terms: Select from highlighted Available Model
Terms.
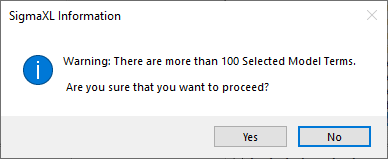
- Select All: Select all Available Model Terms. Caution, the number of selected terms can become quite large, especially for the last two options in the
Term Generator. If more than 100 terms are selected, a warning is given after clicking OK:
- Include Constant: Always checked in GLM.
Tip: It is also important to ensure that the number of rows/observations are sufficient to estimate the number of selected model terms. A rule of thumb (excluding data from a designed experiment) is that for every
term selected, there should be a minimum of 10 rows of data. This rule holds for potential terms used in stepwise and best subsets as well, otherwise one can easily produce a model that is highly significant but a meaningless model
of noise. This is what Jim Frost calls “Data Dredging” in chapter 8 of his book
Regression Analysis: An Intuitive Guide for Using and Interpreting Linear Models.
Example 1: Fixed Factors with Nested Variable
- Open Customer Data.xlsx. Click Sheet 1 Tab. Click
SigmaXL > Statistical Tools > General Linear Model> Fit General Linear Model.
If necessary, click Use Entire Data Table, click Next.
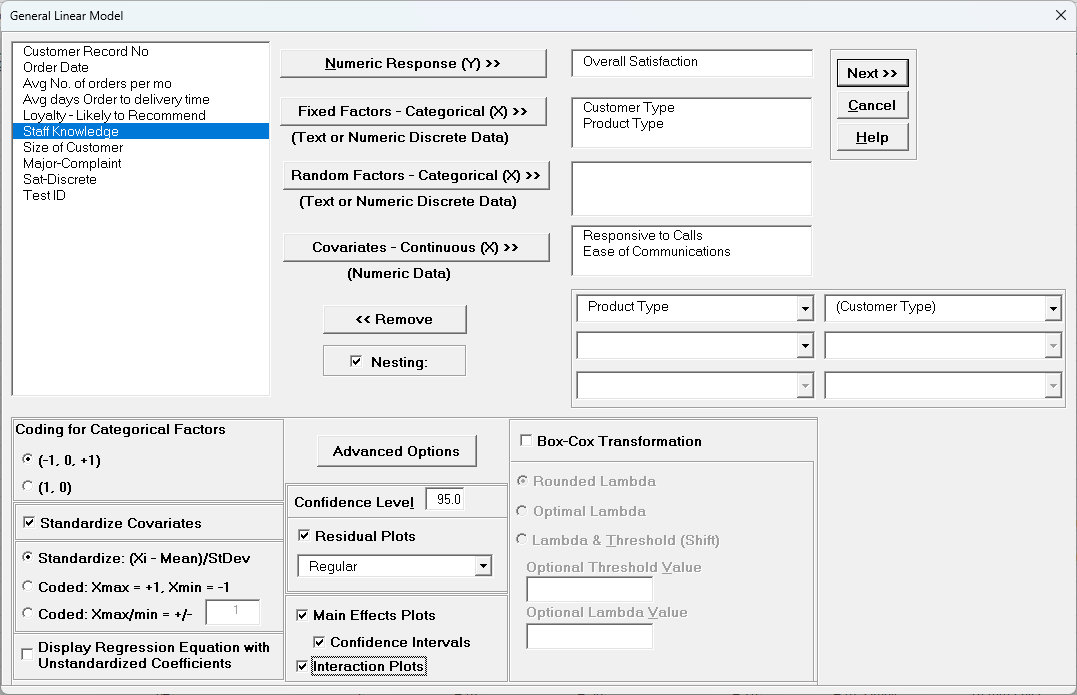
- Select Overall Satisfaction, click Numeric Response (Y) >>, select Customer Type and Product Type, click Fixed Factors - Categorical (X) >>, select Responsive to Calls and Ease of Communications, click Covariates - Continuous (X) >>. Check Nesting.
For the left-side drop-down "Select a Factor or Covariate", select Product Type.
For the right-side drop-down "Select a Factor to Nest in:" select (Customer Type).
We will use the default Coding for Categorical Predictors (-1,0, +1).
Check Standardize Covariates with default option Standardize: (Xi-Mean)/StDev.
Use the default Confidence Level = 95.0%. Regular Residual Plots are checked by default.
Check Main Effects Plots with Confidence Intervals. Leave Interaction Plots and Box-Cox Transformation unchecked.
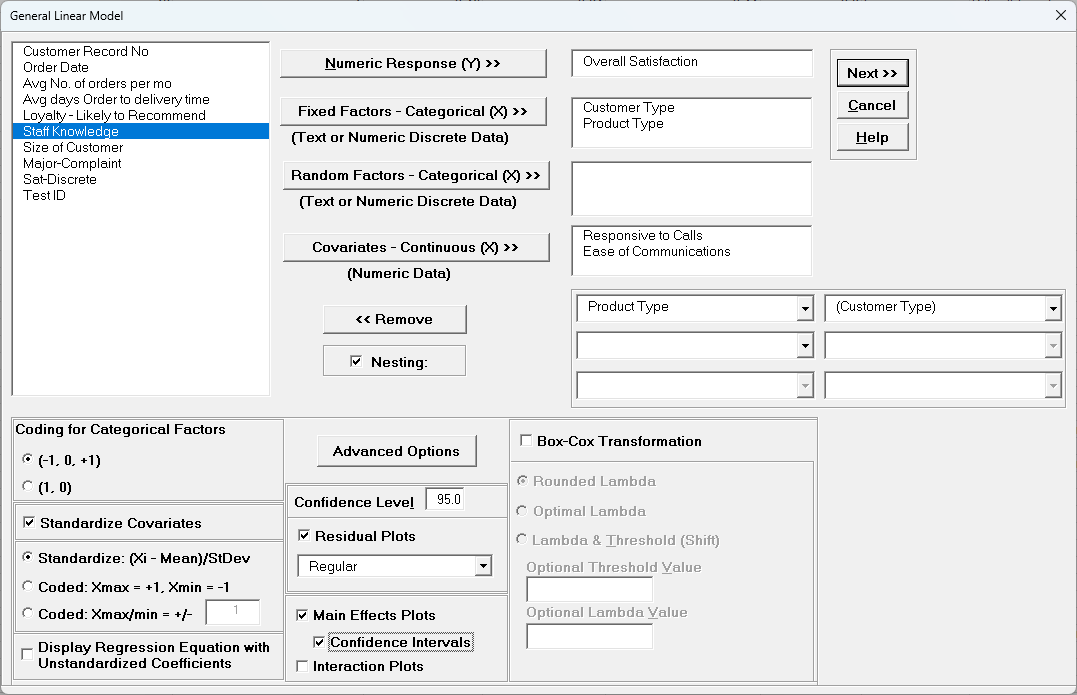
Tip: If you have covariates (continuous predictors) and are planning to include interaction terms in the model, always ensure that Standardize Covariates is checked. This has two benefits: the
covariates are scaled to the same units so coefficients can be meaningfully compared, and it dramatically reduces the multicollinearity VIF scores.
- Click Advanced Options. We will use the default options as shown with
K-Fold Cross Validation and Stepwise/Best Subsets Regression unchecked. Pairwise Comparison of Means for Fixed Factors with
Tukey option is checked.
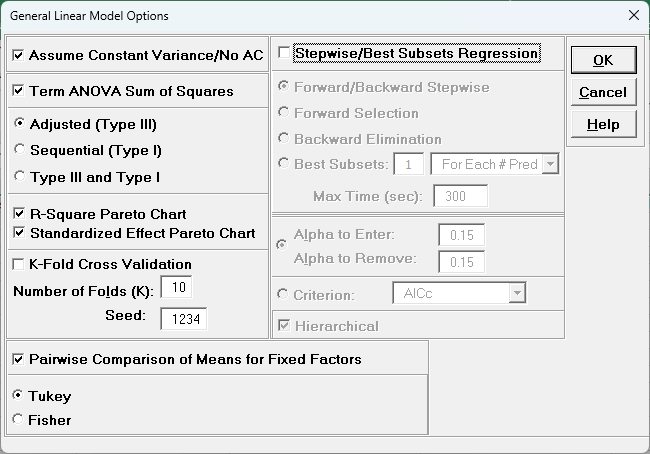
- Click OK. Click Next >>.
- Using Term Generator, select ME + 2-Way Interactions. Select
Responsive to Calls to Responsive to Calls*Ease of Communication. Click
Model Terms >. Include Constant is always checked in General Linear Model.
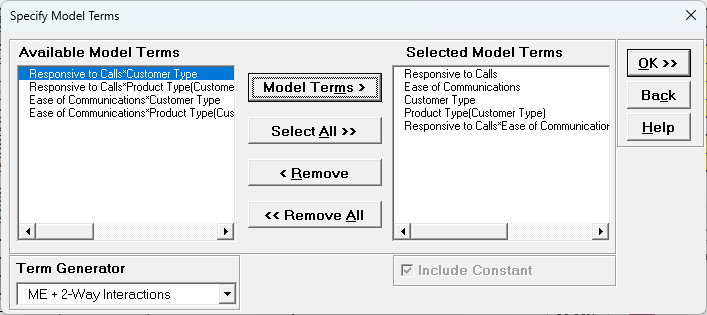
Product Type(Customer Type) denotes that Product Type is nested within
Customer Type. Note, this data is not actually nested, but we are using this as an example to demonstrate nesting with familiar data.
Term Generator, ME + 2-Way Interactions produces only legal two-way interactions, so Product Type*Customer Type is not available for selection. Based on previous regression analysis for Overall Satisfaction, we
are only including the Responsive to Calls*Ease of Communications 2-way interaction.
- Click OK>>. The General Linear Model report is given. The Parameter Estimates - Standardized and ANOVA tables are shown:
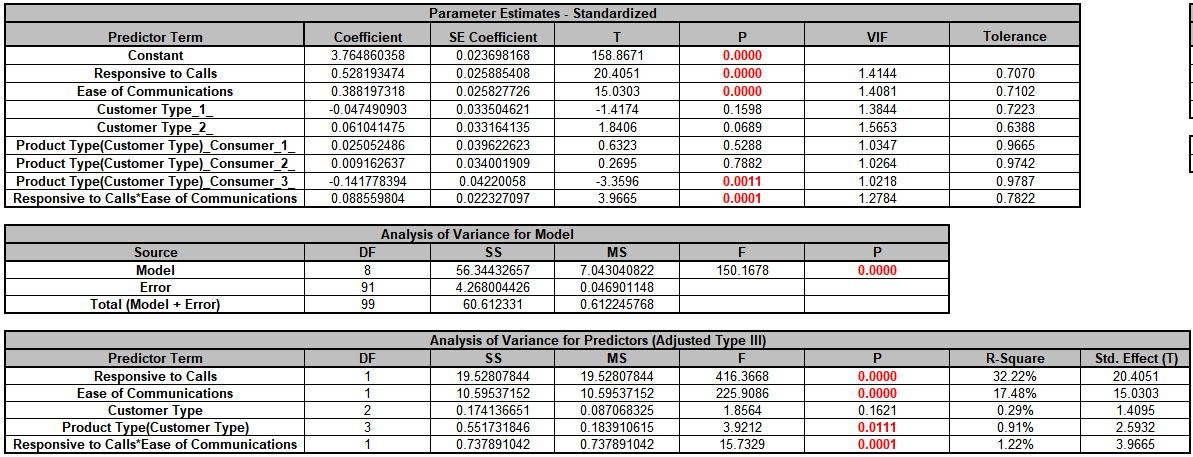
With (-1, 0, 1) coding, the reference level is the last alpha-numerically sorted level. The hidden reference level for Customer Type is 3.
"Product Type(Customer
Type)_Consumer_1_" denotes Product Type Consumer nested within Customer Type 1. The hidden reference level for Product Type is Manufacturer. For further information on nesting see the Appendix: Nested Factors and Coding.
The Analysis of Variance for
Predictors (Adjusted Type III) table shows that Customer Type is not significant with P-Value = 0.162, but we will leave it in the model to maintain hierarchy since Product Type is nested within Customer Type. Product
Type is significant with P-Value = 0.011.
-
The GLM Equation with standardized coefficients is:
General Linear Model: Overall Satisfaction = (3.76486)
+ (0.528193)*((Responsive_to_Calls-3.8644)/1.14029)
+ (0.388197)*((Ease_of_Communications-3.7481)/0.911361)
+ (-0.0474909)*(IF(Customer_Type="1_",1,0)+IF(Customer_Type="3_",-1,0))
+ (0.0610415)*(IF(Customer_Type="2_",1,0)+IF(Customer_Type="3_",-1,0))
+ (0.0250525)*(IF(Product_Type="Consumer",1,0) + IF(Product_Type="",-1,0) + IF(Product_Type="Manufacturer",-1,0))*IF(Customer_Type="1_",1,0)
+ (0.00916264)*(IF(Product_Type="Consumer",1,0) + IF(Product_Type="",-1,0) + IF(Product_Type="Manufacturer",-1,0))*IF(Customer_Type="2_",1,0)
+ (-0.141778)*(IF(Product_Type="Consumer",1,0) + IF(Product_Type="",-1,0) + IF(Product_Type="Manufacturer",-1,0))*IF(Customer_Type="3_",1,0)
+ (0.0885598)*((Responsive_to_Calls-3.8644)/1.14029)*((Ease_of_Communications-3.7481)/0.911361)
Note blanks and special characters in the predictor names are converted to the underscore character "_". The numeric Customer Type 1, 2, 3 has also been converted to text so appear as "1_", "2_", "3_".
For categorical predictors, IF statements are used.
This is the display version of the prediction equation given at cell L14(which has more precision for the coefficients and predictor names are converted
to legal Excel range names by padding with the underscore "_" character). If the equation exceeds 8000 characters (Excel's legal limit for a formula is 8192), then a truncated version is displayed and cell L14does
not show the formula.
-
Scroll to the Predicted Response Calculator. Enter Responsive to Calls and Ease of
Communication values = 5 with Customer Type = 1_ and Product Type = Consumer from the dropdown lists to predict Overall Satisfaction including the 95% confidence interval for the long term mean and 95% prediction interval
for individual values:

-
Next, we will use SigmaXL's built in Optimizer. Scroll to view the Optimize Options:
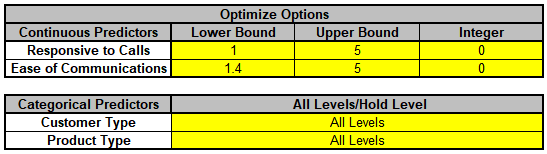
Here we can constrain the continuous predictors and specify a level to use for optimization of the categorical predictors. If a continuous predictor is integer,
change the Integer 0 to 1, and the Optimizer will return only integer values for that predictor.
We will leave the Optimize Option settings as is.
-
Scroll back to view the Goal setting and Optimize button. Select Goal = Maximize.
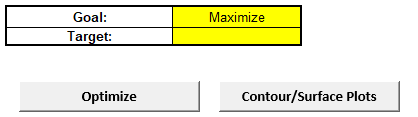
The optimizer uses Multistart Nelder-Mead Simplex to solve for the desired response goal with given constraints. For more information see the Appendix: Single Response Optimization.
-
Click Optimize. The response solution and prompt to paste values into the Input Settings of the Predicted Response Calculator is given:
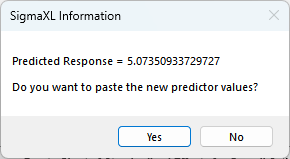
-
Click Yes to paste the values.

The optimizer has selected Customer Type = 3_ and Product Type = Manufacturer to maximize the Overall Satisfaction predicted value.
Note that the optimizer does not test the validity of a nested combination, so if the goal is to optimize, it is best to use generic level names as done in this example. For Product Type, we use the generic levels "Consumer"
and "Manufacturer", not "Consumer_Type1", "Consumer_Type2", "Consumer_Type3"; "Manufacturer_Type1", "Manufacturer_Type2", "Manufacturer_Type3".
- Click on Sheet GLM1 - Pair Comp. The Tukey Pairwise Comparison of Means for Customer Type is shown.

Pairwise comparisons of means examines the difference between all combinations of the estimated means for each category of a factor, along with the standard
error and confidence band for the difference. Tukey provides protection against false positives due to multiple comparisons. Nested factors are not shown in the pairwise comparison report, so Product Type is not included here. For
further information see the Appendix: Pairwise Comparison of Means for Fixed
Factors.
As expected from the ANOVA report, none of the pairwise comparisons are significant.
Click on Sheet GLM1 - Plots. The Main Effects Plots with 95% Confidence Intervals are shown.
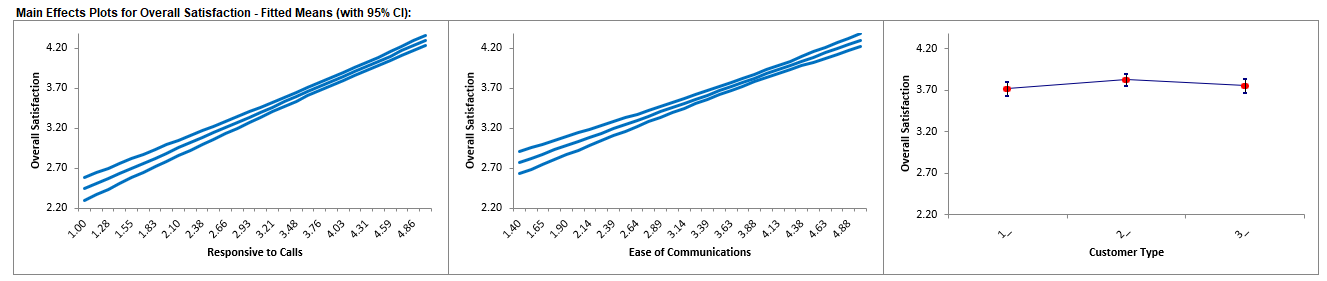
These are based on Fitted Means as predicted by the model, not Data Means. They use the predicted value for the response versus input predictor value, while
holding all other variables constant. Continuous are held at their respective means and categorical are weighted equally.
Here we see that Responsive to Calls has the steepest slope followed by Ease of Communications. As expected, Customer Type does not appear to be an important factor.
Example 2: Sources of Variation Study
Open We will now reanalyze the Multi-Vari data presented in Multi-Vari
Charts. The Multi-Vari chart was used to identify dominant Sources of Variation (SOV), with the three major “families” of variation being Within Unit, Between Unit, and Temporal (Over
Time).
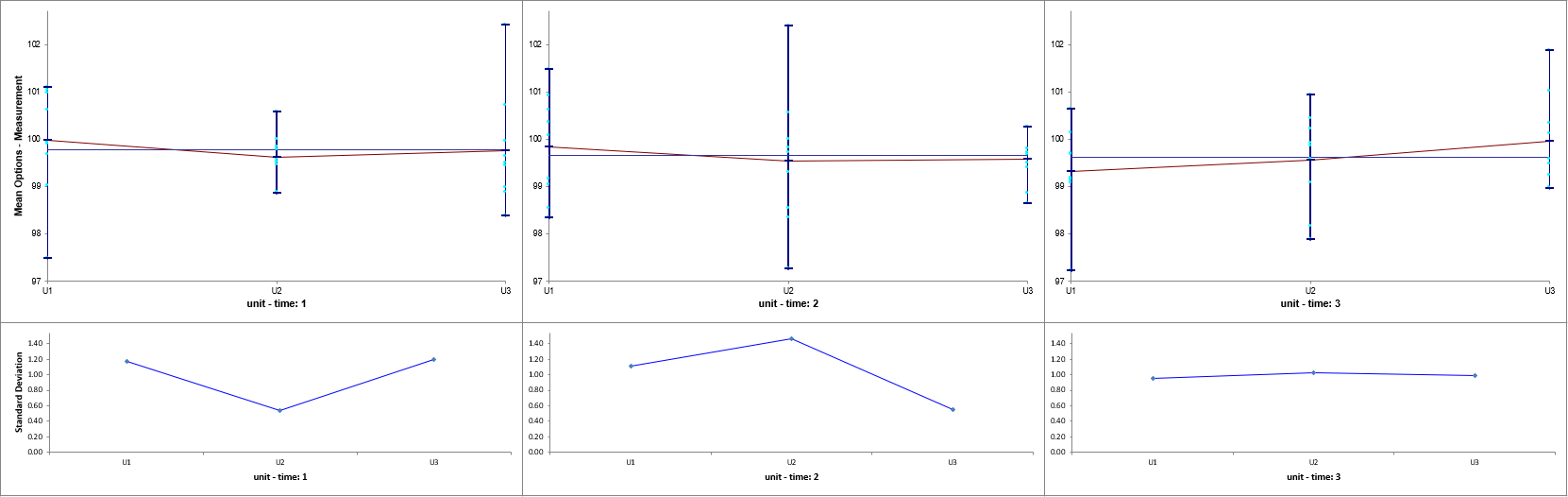
Dominant “Within Unit” Source of Variation:
Dominant “Between Unit” Source of Variation:
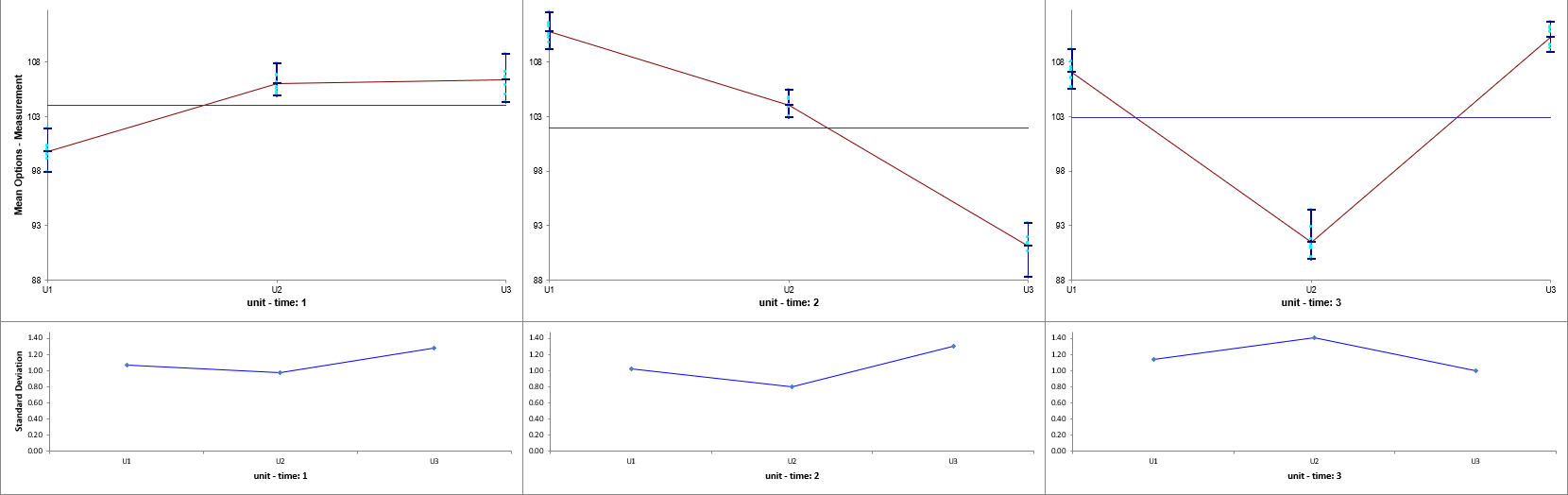
Dominant “Over Time” Source of Variation:
Unit and Time are Random Factors and Unit is nested within
Time. The Variance Components will be calculated to quantify the percent contribution to total variation for each factor.
-
Open Multi-Vari Data.xlsx, click Sheet Within. Click
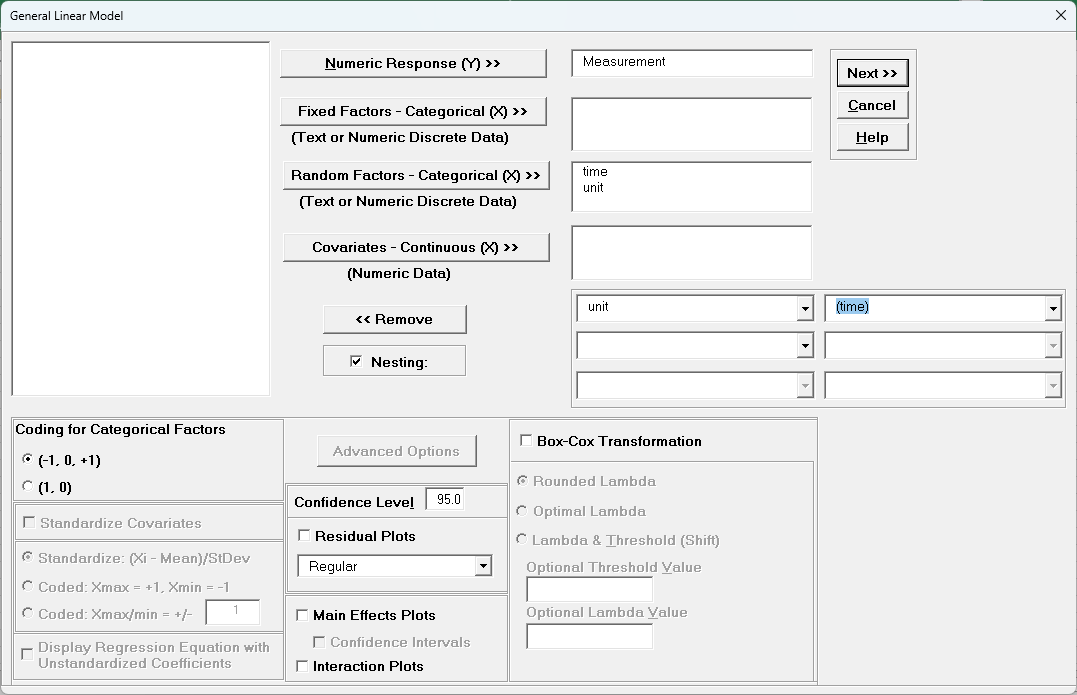
SigmaXL > Statistical Tools > General Linear Model > Fit General Linear Model. If necessary, click Use Entire Data Table, click Next.
-
Select Measurement, click Numeric Response (Y) >>, select
time, click Random Factors - Categorical (X) >>, select
unit, click Random Factors - Categorical (X) >>. Check Nesting. For the left-side drop-down “Select a Factor or Covariate”, select unit. For
the right-side drop-down “Select a Factor to Nest in:“, select
(time). We will use the default Coding for Categorical Predictors (-1,0,
+1) and default Confidence Level = 95.0%. Leave Residual
Plots, Main Effects Plots, Interaction Plots and Box-Cox
Transformation unchecked. Advanced Options are not available with Random Factors.
-
Click Next >>.
-
Leave Term Generator as Main Effects. Click Select All >>. (If the order is reversed, select time, click Model Terms >, select
unit(time), click Model Terms >.)
The term
unit(time) denotes that unit is nested within time. Since time is the top level of the nesting, we place it in the model first.
-
Click OK >>. The Variance Components report is given:
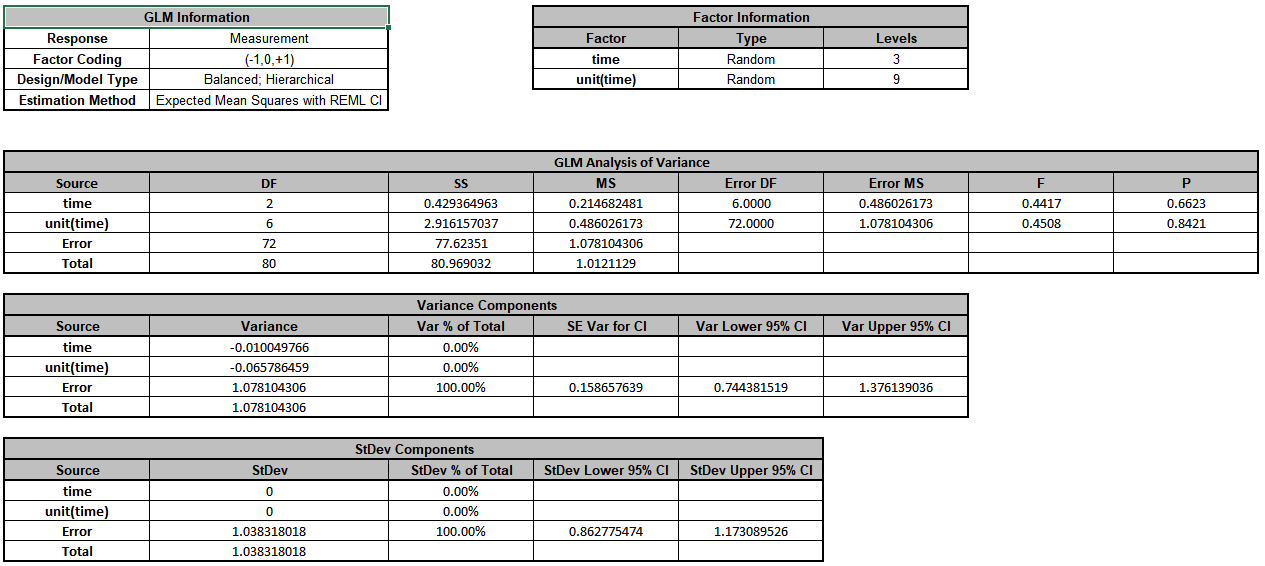
The
Error term in the variance components table is the “Within Unit” variation. It is contributing to 100% of the total variation. The REML 95% confidence interval for this variance component
is also given.
The terms time and unit(time) have negative Variance Component values, so are treated as 0. The ANOVA table shows that both terms are not significant random factors (alpha = 0.05). Standard Deviation
components are provided for convenience and useful in Measurement Systems Analysis, but they will not be discussed here.
The GLM Model sheet is the regression analysis but we will not review that here as our focus is on the variance components analysis. Note that the regression analysis treats random factors as fixed.
-
Now click sheet Between. Repeat steps 1 to 5 to produce the Variance Components report:
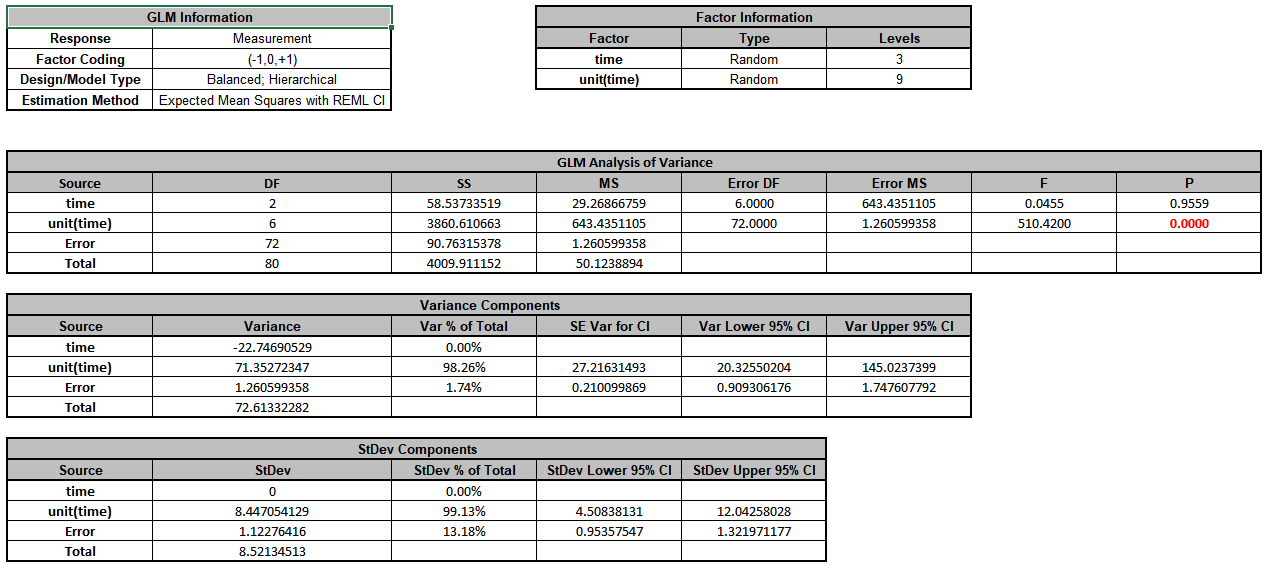
The
unit(time) term in the variance components table is the “Between Unit” variation. It is contributing to 98.3% of the total variation. The “Within Unit” Error term is contributing to 1.7% of the total variation. The REML 95% confidence interval for these variance components are also given.
The term time has a negative Variance Component value, so is treated as 0. The ANOVA table shows that time is not a significant random factor, but unit(time) is significant (alpha = 0.05).
-
Now click sheet Over Time. Repeat steps 1 to 5 to produce the Variance Components report:
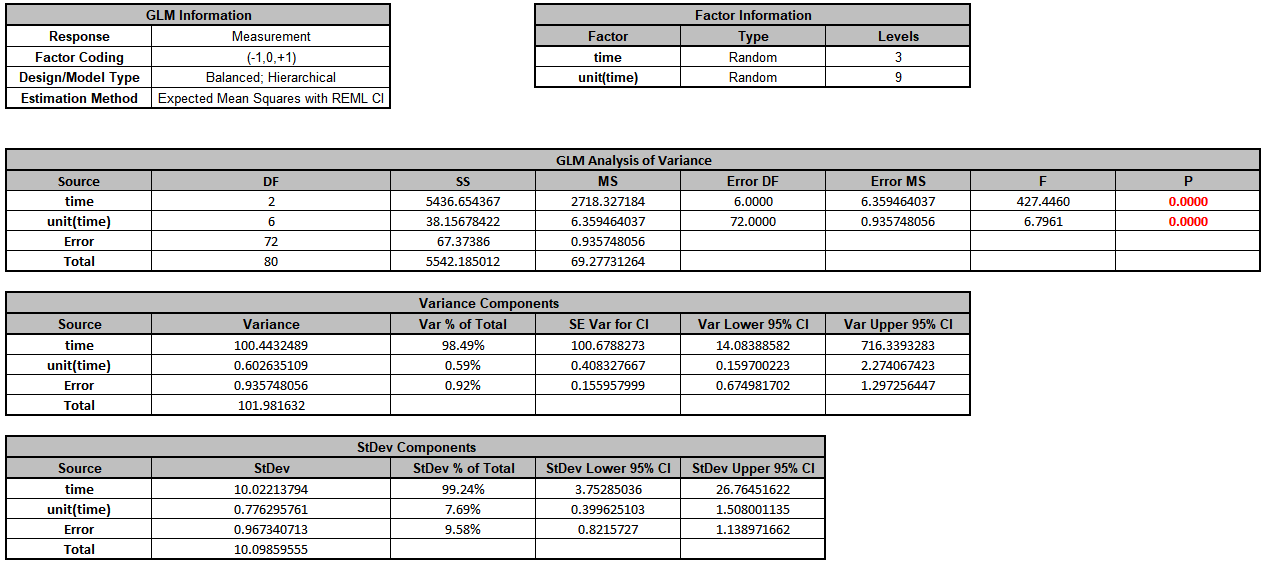
The
time term in the variance components table is the “Over Time” variation. It is contributing to 98.5% of the total variation. The “Between Unit” unit(time) term is contributing to 0.6% of the total variation. The
“Within Unit” Error term is contributing to 0.9% of the total variation. The REML 95% confidence interval for these variance components are also given. Note that the confidence interval for time is very wide. This is due to only having 3 levels. If possible, additional time value data should be collected in order to reduce the uncertainty of the variance component value.
The ANOVA table shows that time and unit(time) are significant random factors (alpha = 0.05).
Example 3: Classical Gage R&R Study
We will now reanalyze the AIAG Gage R&R data presented in Analyze Gage R&R
(Crossed). The Gage R&R Study Report was given as:
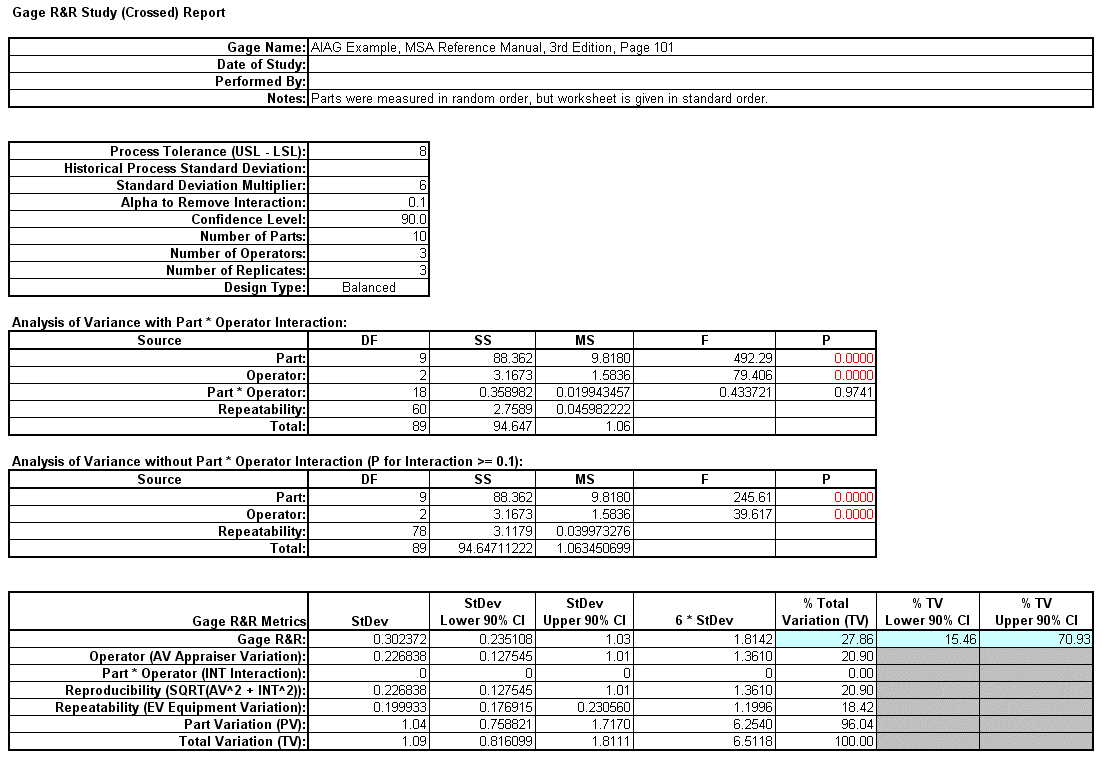
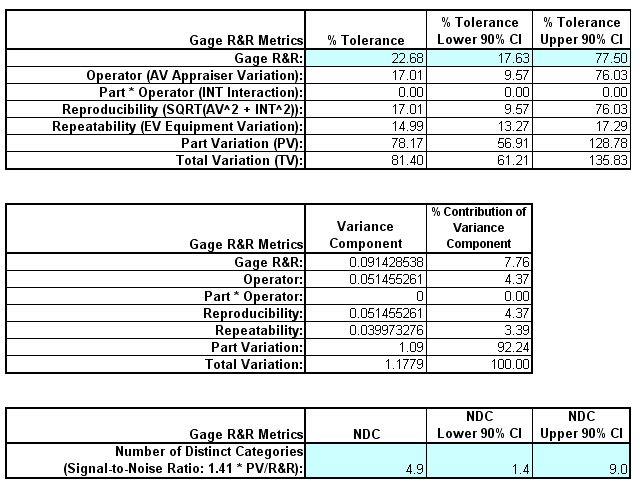
- Open the file Gage RR - AIAG.xlsx. This is an example from the Automotive Industry Action Group (AIAG) MSA Reference Manual, 3rd Edition, page 101. Note that parts were measured in random order, but the worksheet is
given in standard order. Preselect the worksheet data including column headings. Click
SigmaXL > Statistical Tools > General Linear Model > Fit General Linear Model. Click Next >>.
- Select Measurement, click Numeric Response (Y) >>, select
Part and Operator, click Random Factors - Categorical (X) >>. Leave Nesting unchecked. We will use the default Coding for Categorical Predictors (-1,0, +1). Set
the
Confidence Level = 90% to match the previous Gage R&R analysis. Leave
Residual Plots, Main Effects Plots, Interaction Plots and Box-Cox
Transformation unchecked. Advanced Options are not available with Random Factors.
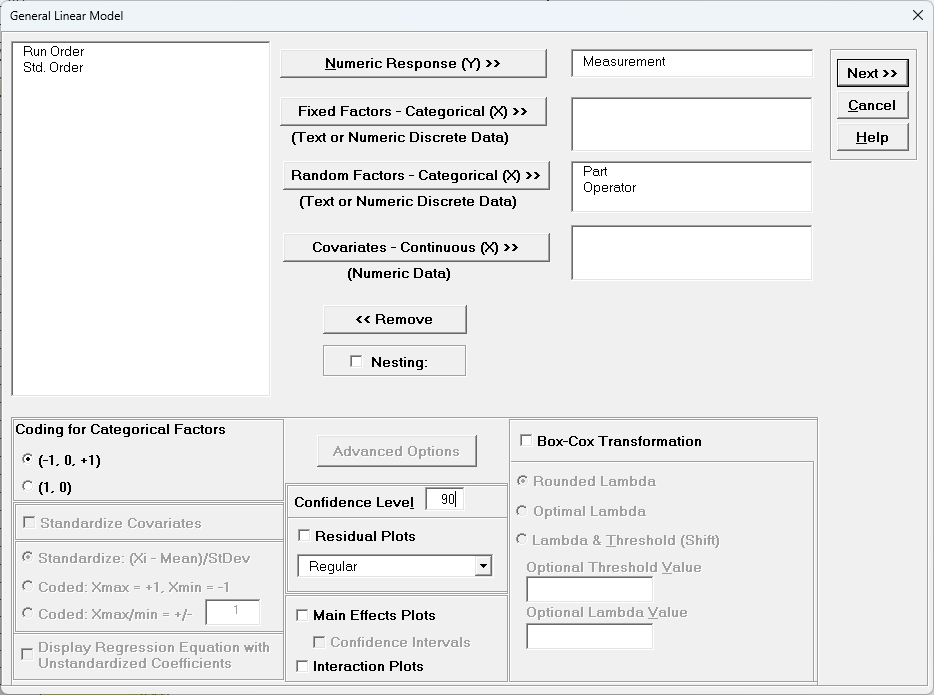
- Click Next >>.
- Using Term Generator, select ME + 2-Way Interactions. Click
Select ALL >>. Include Constant is always checked in General Linear Model.
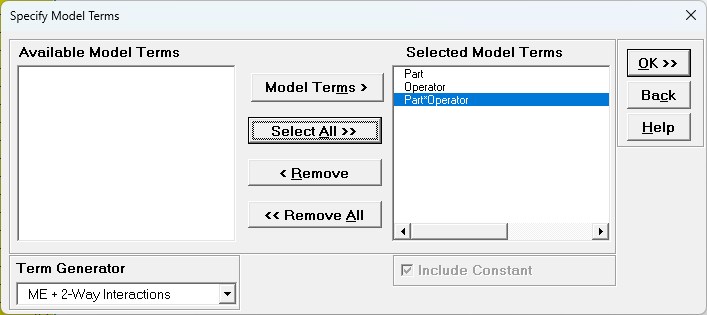
- Click OK >>. The Variance Components report is given:
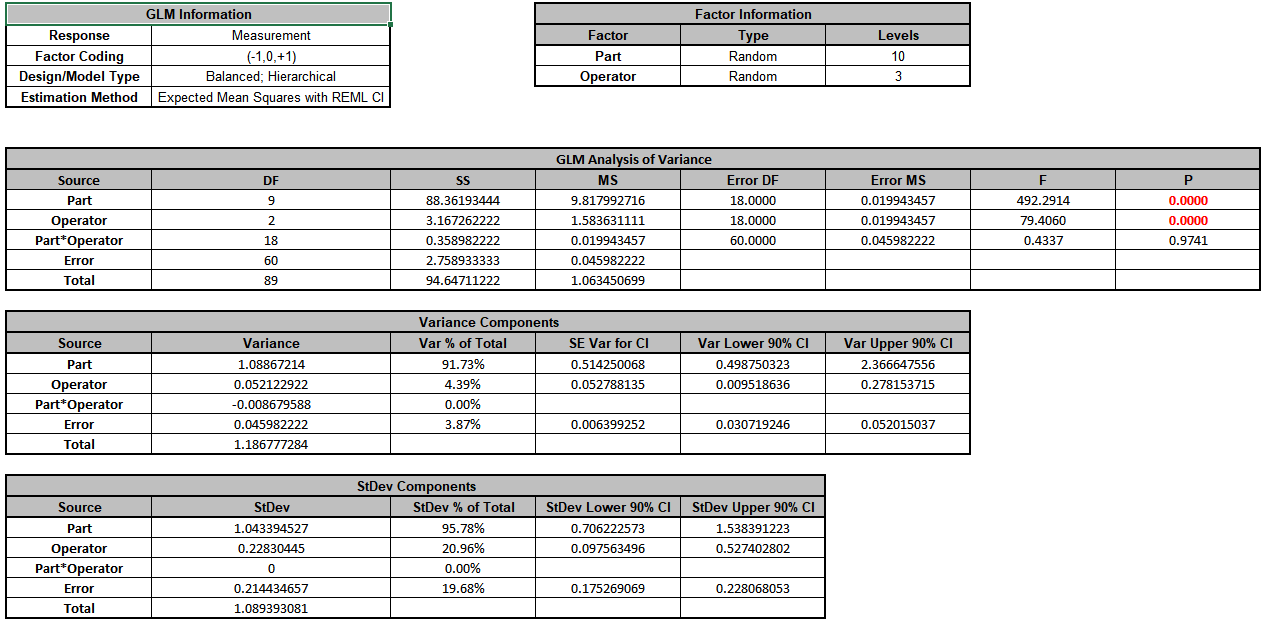
- Since the Part*Operator interaction term is not significant (alpha = 0.1), we will refit the model excluding this term. Press F3 or click Recall SigmaXL
Dialog to recall last dialog.
- Click Next >>. Select Part*Operator, click
< Remove.
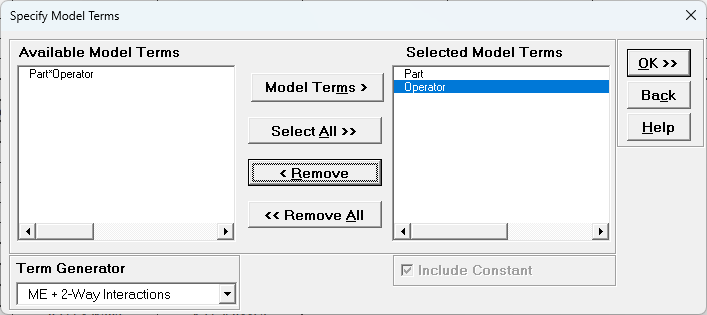
- Click OK>>. The revised Variance Components report is shown:
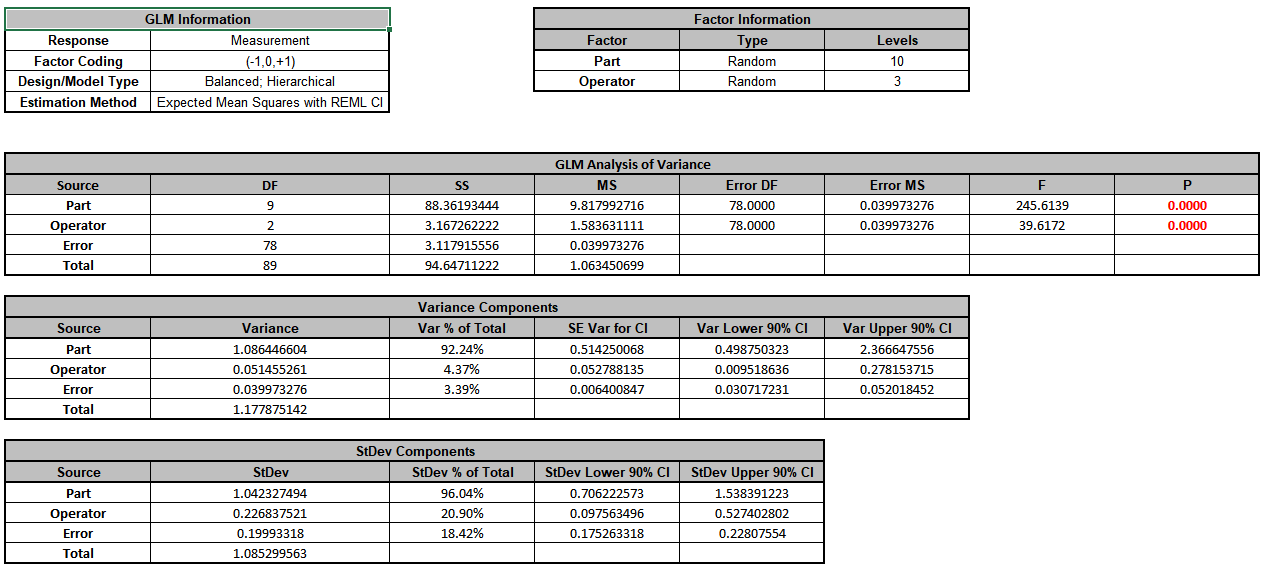
- Now we will now convert the GLM Variance Components to Gage R&R Metrics. Click on
SigmaXL > Measurement Systems Analysis > Basic MSA Templates > GLM GageRR (Crossed)
Metrics without Interaction to open the conversion template.
- Copy the Variance Component values in cells C18:C20 (Sheet GLM2 –
VarComp) and paste the values into the yellow highlighted cells
C15:C17 of the template. For Gage Name, enter the information as shown. Enter Process Tolerance =8, use Standard Deviation Multiplier = 6.
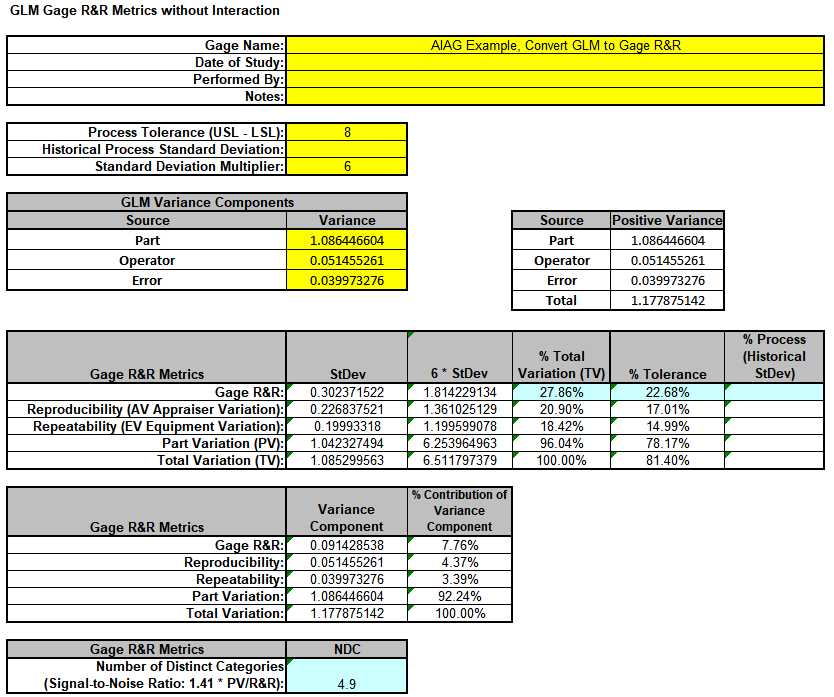
Warning: It is crucial to ensure that the GLM Variance Components Source Names match those given in the template. If the GLM model order was different than that of the template, each entry would have to be
copy/pasted individually.
- This template converts the GLM Variance Components to Gage R&R metrics. The results match those given in the original analysis, excluding the confidence intervals and ANOVA table. With %Total Variation and %Tolerance less than 30%
but greater than 10%, this is a marginal measurement system.
- Next, we will show examples where the classical Gage R&R Analysis does not work and GLM is required to do the analysis.
Example 4: Gage R&R Study with Operator as Fixed Factor
We will reanalyze the AIAG Gage R&R data above, but now we will treat Operator as a Fixed Factor. In this case “Operator” could denote a test fixture and there are only three of them in the plant.
- Open the file Gage RR - AIAG.xlsx. Preselect the worksheet data including column headings. Click SigmaXL > Statistical Tools > General Linear Model > Fit General
Linear Model. Click Next>>.
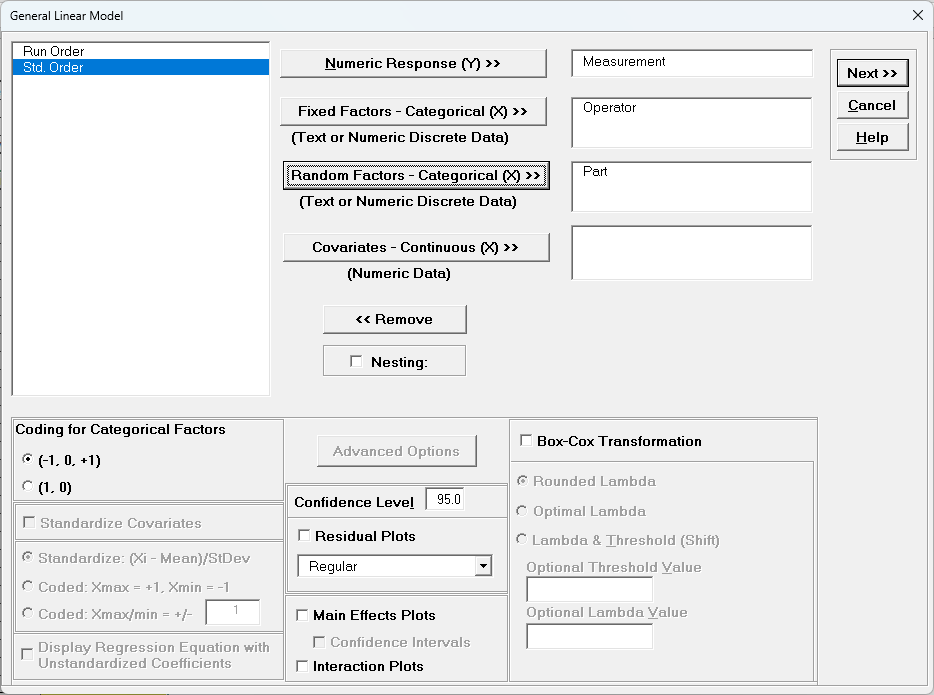
- Select Measurement, click Numeric Response (Y) >>, select
Operator, click Fixed Factors - Categorical (X) >>, select Part, click Random Factors - Categorical (X) >>. Leave Nesting unchecked. We will use the default Coding for Categorical Predictors (-1, 0, +1) and default
Confidence Level = 95.0%. Leave Residual Plots, Main Effects Plots,
Interaction Plots and Box-Cox Transformation unchecked.
Advanced Options are not available with Random Factors.
-
Click Next >>.
-
Leave Term Generator as Main Effects. Click Select ALL
>>.
-
Click OK >>. The Variance Components report is given:
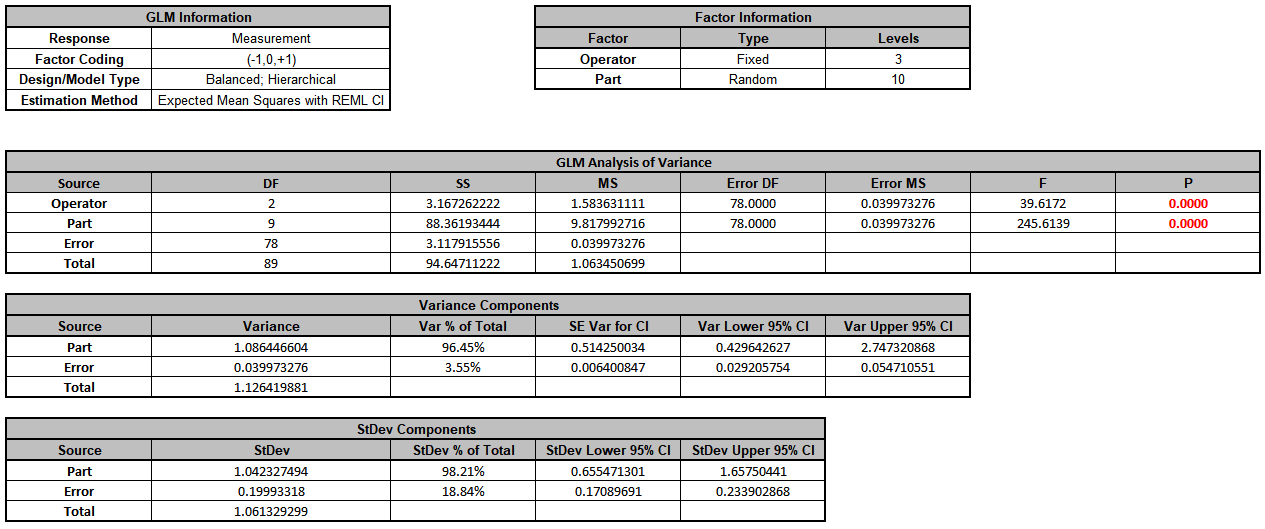
Note that Operator is no longer in the Variance Components table. We will need to manually calculate the VC value to be entered into the GLM GageRR template.
-
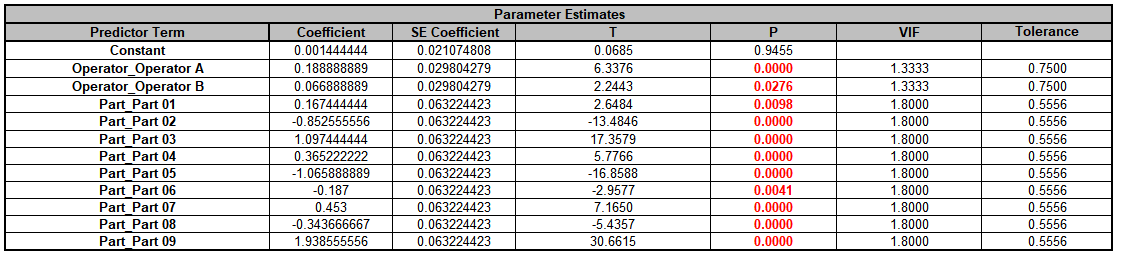
Click on Sheet GLM# Model for the current model. The Parameter Estimates are given as:
-
The coded (-1, 0, 1) coefficients for Operator will be used to estimate the Fixed Factor Variance Component. It is the average of the coefficients squared, including the hidden reference value. (This is from Formula
6.2 in Burdick, R. K., Borror, C. M., and Montgomery, D. C., “Design and Analysis of Gauge R&R Studies: Making Decisions with Confidence Intervals in Random and Mixed ANOVA Models”, ASA-SIAM
Series on Statistics and Applied Probability, 2005.) Note, this calculation cannot be done with coded (0, 1) coefficients.
Operator C coefficient (hidden reference) = -(0.18889 + 0.06689) = - 0.25578
Fixed Operator VC =((0.18889)^2 + (0.06689)^2 + (-0.25578)^2)/3 = 0.035192.
Use Excel formulas to calculate this to full precision.
-
Now we will now convert the GLM and Manual Variance Components to Gage R&R Metrics. Click on
SigmaXL > Measurement Systems Analysis > Basic MSA Templates > GLM GageRR (Crossed)
Metrics without Interaction to open the conversion template.
-
Enter the Variance Component values into the yellow highlighted cells C15:C17 of the template as shown. For Gage Name, enter the information as shown. Enter Process Tolerance =8, use Standard Deviation Multiplier
= 6.
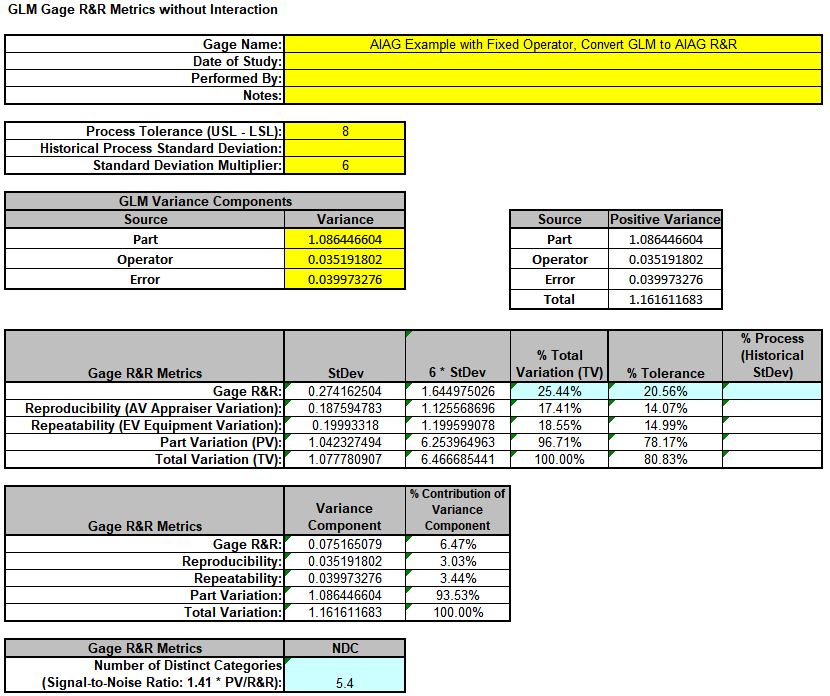
Warning: It is crucial to ensure that the GLM Variance Components Source Names match those given in the template.
-
This template converts the GLM Variance Components to Gage R&R metrics. Note that the %Total Variation has been reduced from the original 27.86% to 25.44%, %Tolerance from 22.68% to 20.56% and NDC increased from 4.9 to 5.4. However, it is still considered
a marginal measurement system. Note that these steps should only be done when Operator is a fixed factor.
Example 5: Gage R&R Study with Operator and One Part
We will reanalyze the AIAG Gage R&R data, but now we will consider the case where there is only one part, i.e., like a Type 1 Gage R&R Study but with multiple operators.
- Open the file Gage RR – AIAG.xlsx. Preselect the worksheet data including column headings. Click Excel > Data > Filter, select Part, uncheck Select All, check Part 01 as shown.
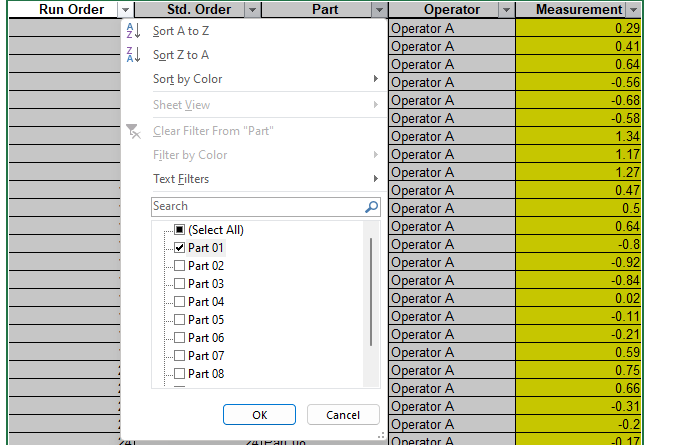
- Click OK. This hides the rows for Parts 02 to 10.
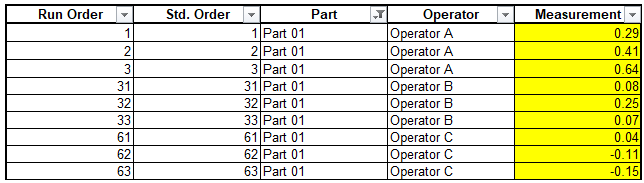
Note: Three measurement readings per operator for a study with one part is not recommended. We are using this example with the AIAG data for convenience.
- Click SigmaXL > Statistical Tools > General Linear Model > Fit General Linear Model. Click Next >>.
- Select Measurement, click Numeric Response (Y) >>, select Operator, click Random Factors - Categorical (X) >>.
Leave Nesting unchecked.
We will use the default Coding for Categorical Predictors (-1, 0, +1) and default Confidence Level = 95.0%. Leave Residual Plots, Main Effects Plots, Interaction Plots and Box-Cox Transformation unchecked.
Advanced Options are not available with Random Factors.
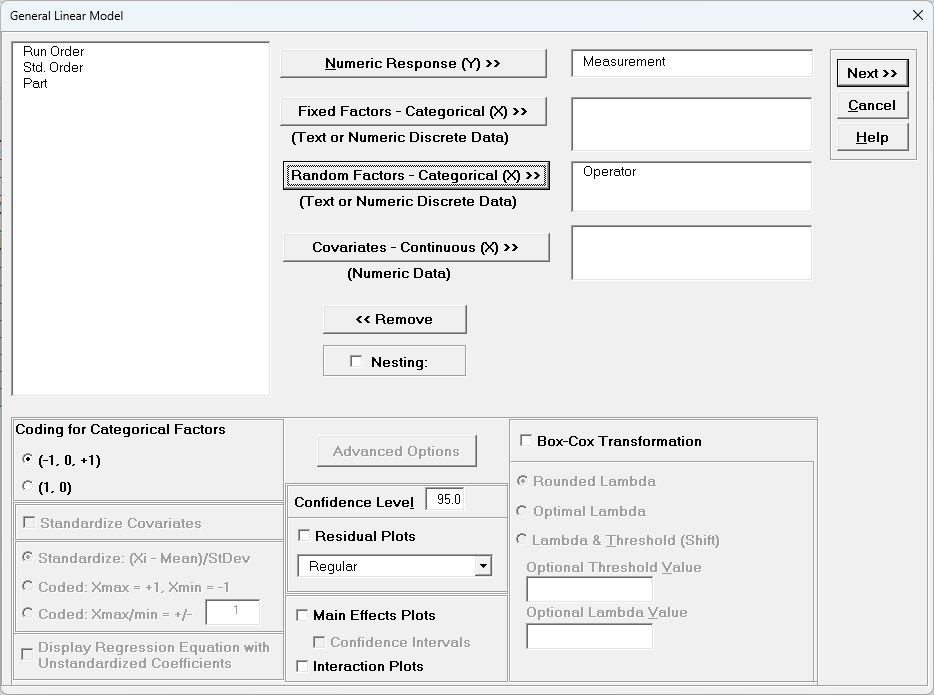
- Click Next >>.
- Click Model Terms >>.
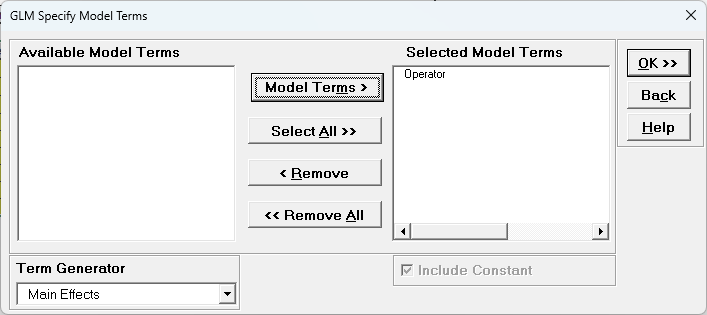
- Click OK >>. The Variance Components report is given:
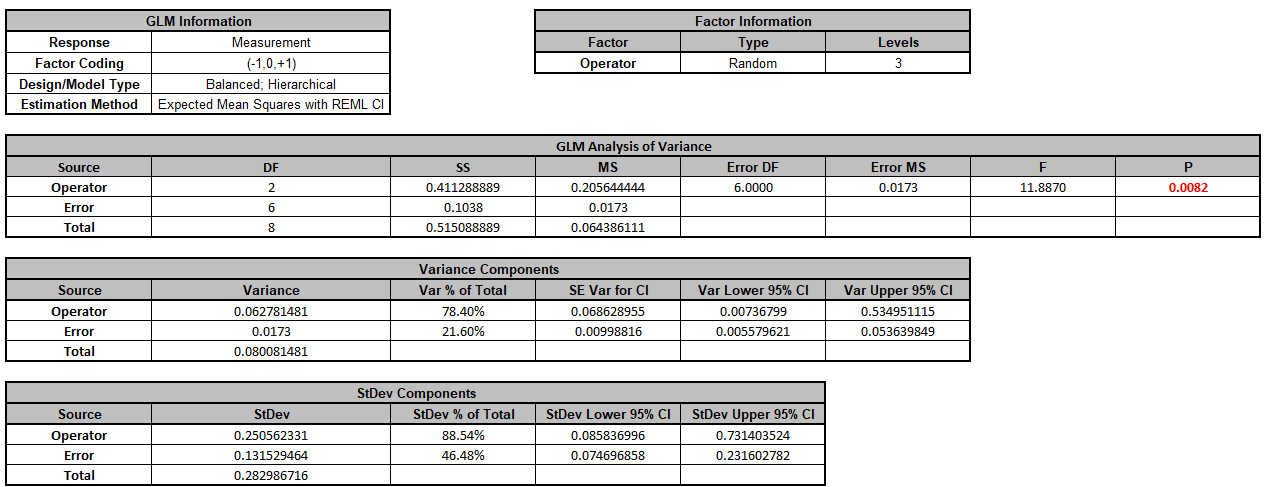
- Now we will now convert the GLM and Manual Variance Components to Gage R&R Metrics.
Click SigmaXL > Measurement Systems Analysis > Basic MSA Templates > GLM GageRR (Crossed) Metrics without Interaction to open the conversion template.
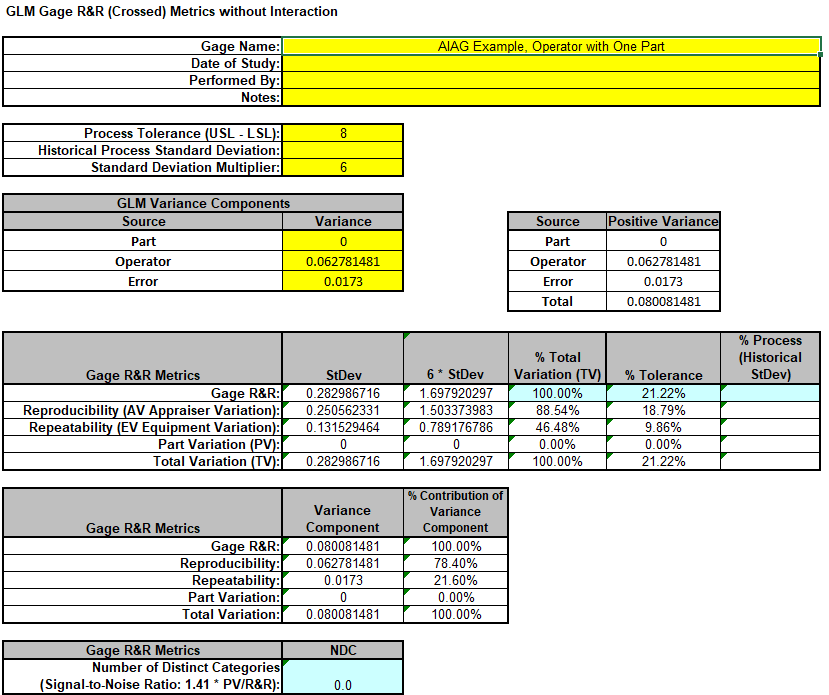
- Copy the Variance Component values in cells C16:C17 (Sheet GLM# – VarComp) and paste the values into the yellow highlighted cells C16:C17 of the template.
Enter 0 for Part Variance.
For Gage Name, enter the information as shown. Enter Process Tolerance =8, use Standard Deviation Multiplier = 6.
Warning: It is crucial to ensure that the GLM Variance Components Source Names match those given in the template.
- This template converts the GLM Variance Components to Gage R&R metrics.
The %Total Variation is not applicable here because there is no part variation.
With %Tolerance less than 30% but greater than 10%, this is a marginal measurement system.
Example 6: Destructive (Nested) Gage R&R
We will now analyze data from a Destructive (Nested) Gage R&R found in the paper referenced below with link to the PDF. This is a shear test for a resistance spot welding process. Design of Experiments were used to produce the parts
by varying preheat temperature, preheat current, welding temperature and welding current. Each run of a 4 Factor 8-Run Fractional Factorial DOE is a “Part” and this was replicated 6 times for
a total of 48 welds. Two Shear Test machines were used so each machine tested 8 Parts with 3 Replicates. The shear test machines are the “Operator” and treated as a random factor in the study.
Tensile Shear Strength (TSS Newtons) and Ultimate Strain (US mm) were measured, but we will only consider TSS here.
Reference: Almeida, F., Gomes, G., Sabioni, R., Gomes, J., de Paula, V., de Paiva, A., & da Costa, S. (2018)."A Gage Study Applied in Shear Test to Identify Variation Causes from a Resistance Spot Welding Measurement
System", Strojni'kivestnik
- Journal of Mechanical Engineering, 64(10), 621-631. https://www.sv-jme.eu/?ns_articles_pdf=/ns_articles/files/ojs/5235/public/5235-30318-1-PB.pdf&id=6160
-
Open the file Tensile Shear Strength.xlsx. Click SigmaXL > Statistical
Tools > General Linear Model > Fit General Linear Model. If necessary, click
Use Entire Data Table, click
Next.
- Select TSS, click Numeric Response (Y) >>, select Operator, click
Random Factors - Categorical (X) >>, select Part, click Random
Factors - Categorical (X) >>. Check
Nesting. For the left-side drop-down “Select a Factor or Covariate”, select
Part. For the right-side drop-down “Select a Factor to Nest in:”, select
(Operator). We will use the default Coding for Categorical Predictors (-1, 0,
+1) and default Confidence Level = 95.0%. Leave Plots,
Main Effects Plots, Interaction Plots and Box-Cox Transformation unchecked. Advanced Options are not available with Random Factors.
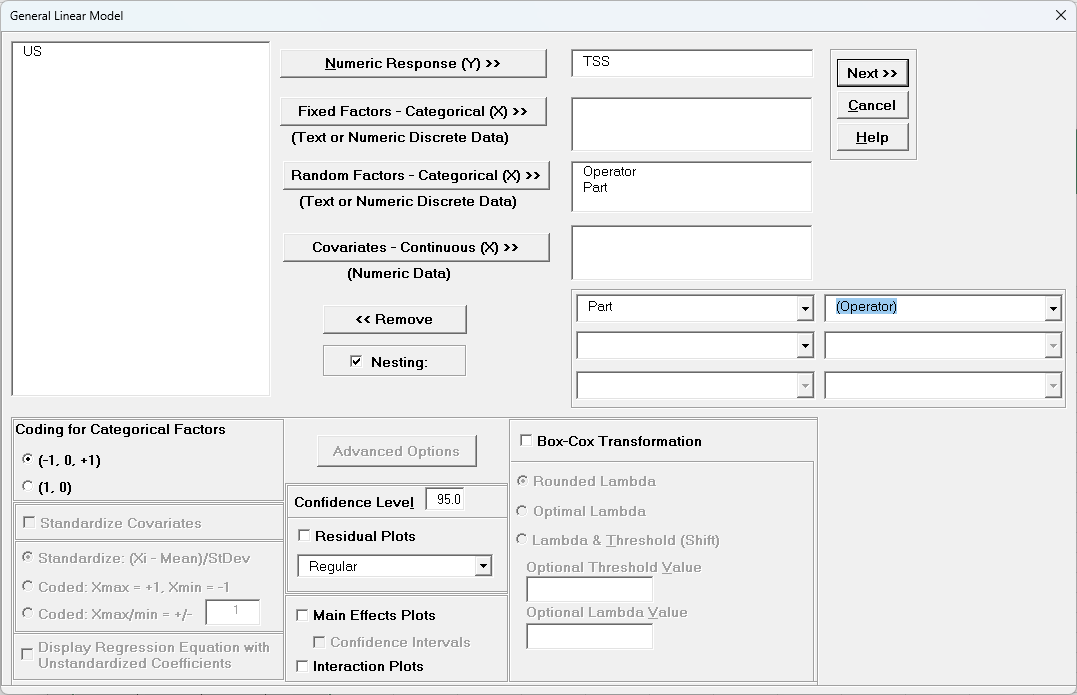
- Click Next >>.
- Leave Term Generator as Main Effects. Click Select ALL
>>.
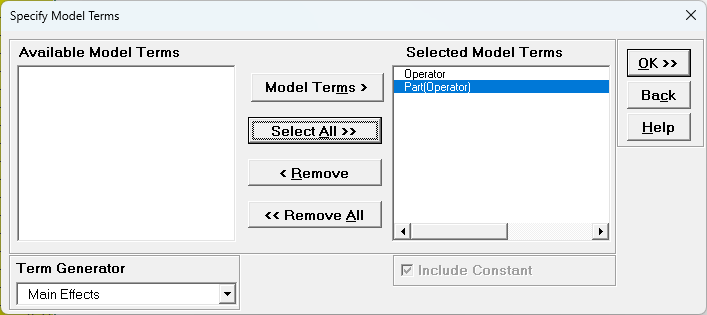
The term Part(Operator) denotes that Part is nested within
Operator. Since Operator is the top level of the nesting, we place it in the model first.
- Click OK >>. The Variance Components report is given:
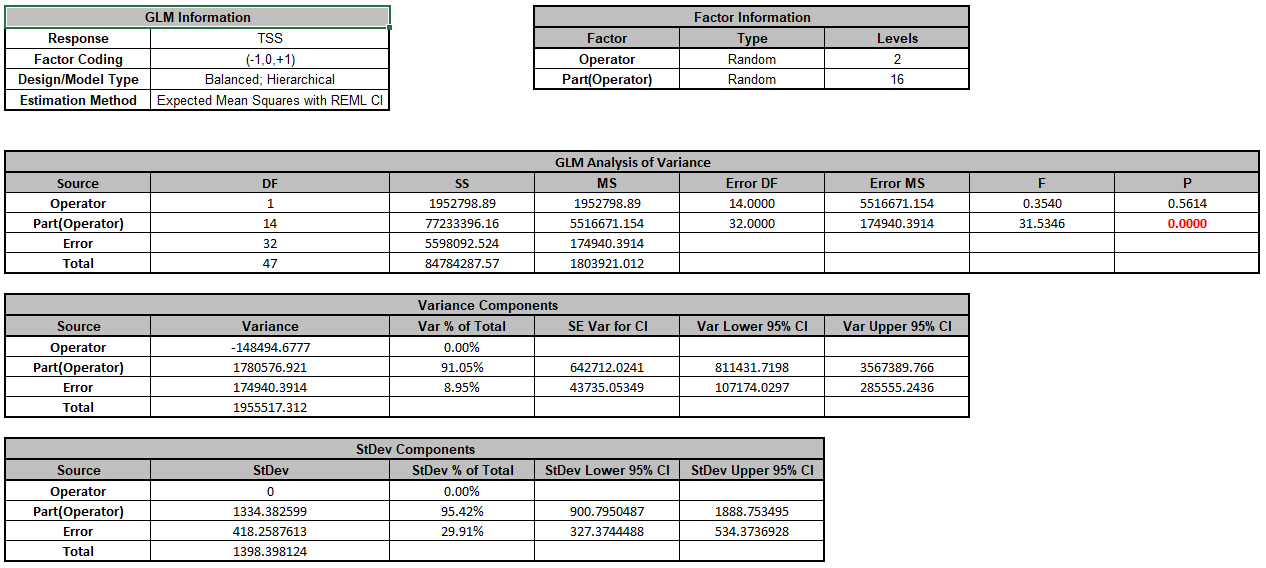
Note that Operator is a negative variance component. It will be treated as zero.
- Now we will now convert the GLM Variance Components to Gage R&R Metrics. Click on
SigmaXL > Measurement Systems Analysis > Basic MSA Templates > GLM GageRR (Nested)
Metrics to open the conversion template.
- Copy the Variance Component values in cells C18:C20 (Sheet GLM1 -
VarComp) and paste the values into the yellow highlighted cells C15:C17
of the template. For Gage Name, enter the information as shown. Use Standard Deviation Multiplier = 6.
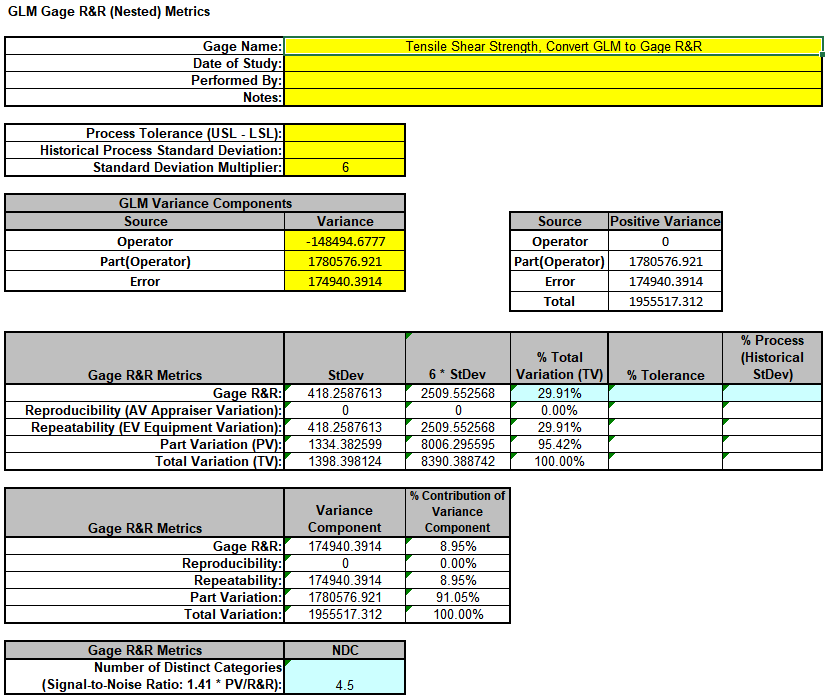
Warning: It is crucial to ensure that the GLM Variance Components Source Names match those given in the template. If the GLM model order was different than that of the template, each entry would have to be copy/pasted
individually.
- This template converts the GLM Variance Components to Gage R&R metrics. With %Total Variation less than 30% but greater than 10%, this is a marginal measurement system. The results match those given in the paper.
Example 7: Expanded Gage R&R
We will now analyze data from an Expanded Gage R&R found in the paper referenced below with link to the PDF. This is a wafer thickness measurement (Angstroms) for a semiconductor process. The design includes random factors: Batch,
Wafer, Location and Operator. Wafer is nested within Batch and Location is nested within Wafer. There are 3 Batches, 3 Wafers, 4 Locations, 3 Operators and 2 Replicates for a total of 216 thickness measurements. The variance components
for Part/Process include Batch, Wafer(Batch) and Location(Wafer(Batch)). The variance components for Reproducibility include Operator, Batch*Operator, Wafer(Batch)*Operator and Location(Wafer(Batch))*Operator. The variance component
for Repeatability is the Error term from Replicates.
Reference: Lee, S.H., Lee, C.W. (2005), “A Study of Gage R&R Analysis Considering the Variations of Between-Within Group and Within Part” IE Interfaces 18(4), 444-453. https://koreascience.kr/article/JAKO200529256810322.pdf. Written in Korean but abstract, formulas, figures and tables are in English.
-
Open the file Wafer Thickness.xlsx. Click SigmaXL > Statistical Tools
> General Linear Model > Fit General Linear Model. If necessary, click Use
Entire Data Table, click Next.
-
Select Thickness, click Numeric Response (Y) >>, select Batch to
Operator, click Random Factors - Categorical (X) >>. Check
Nesting. For the left-side drop-down “Select a Factor or Covariate”, select Wafer. For the right-side drop-down “Select a Factor to Nest in:”,
select (Batch). For the second left-side drop-down “Select a Factor or Covariate”, select Location. For the right-side drop-down “Select a Factor to Nest in:”,
select (Wafer). We will use the default Coding for Categorical
Predictors (-1, 0, +1) and default Confidence Level = 95.0%. Leave Residual Plots, Main Effects Plots, Interaction Plots and
Box-Cox Transformation unchecked. Advanced Options are not available with Random Factors.
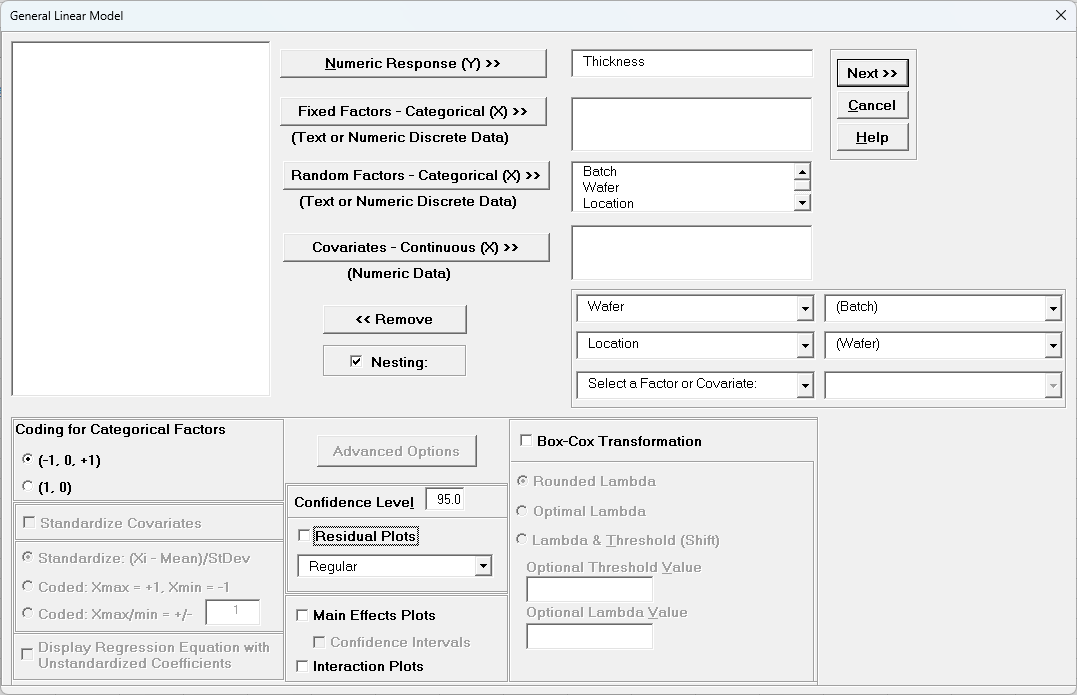
- Click Next >>.
- Using Term Generator, select ME + 2-Way Interactions. Click Select ALL >>.
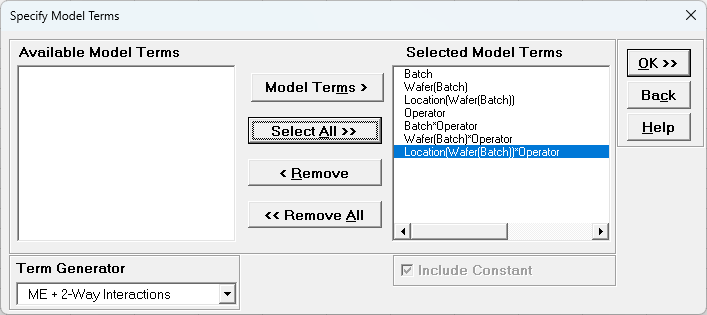
The term Wafer(Batch) denotes that Wafer is nested within Batch. The term Location(Wafer(Batch)) denotes that Location is nested within Wafer which is nested within Batch. Only legal 2-Way Interactions are available, so Wafer*Batch, Location*Wafer or Location*Batch are not available.
- Click OK >>. The Variance Components report is given:
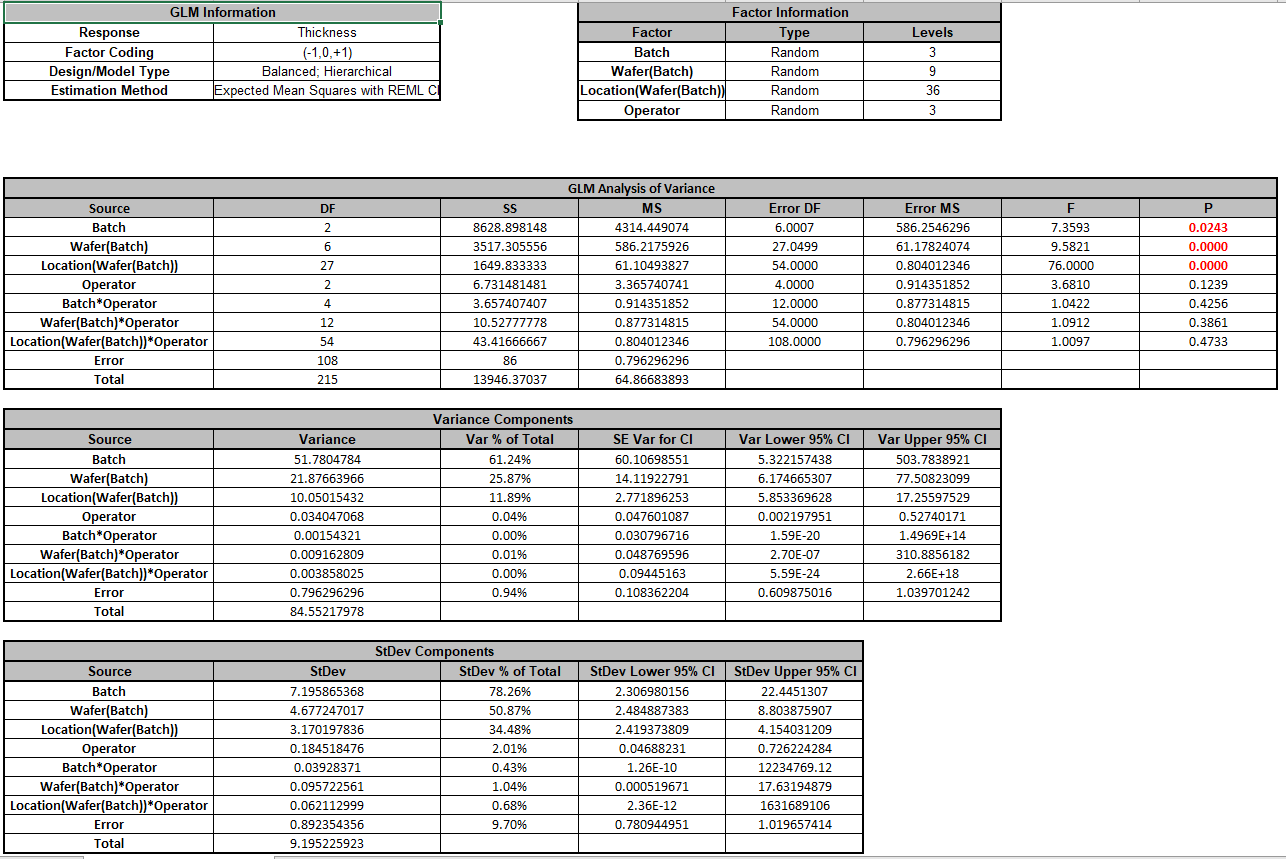
Note that the variance component confidence intervals for the interaction terms with Operator are very wide and the P-Values are insignificant (alpha = 0.05), so the model could be refit excluding these terms but we will not do
so here.
- Now we will now convert the GLM Variance Components to Gage R&R Metrics. Click on SigmaXL > Measurement Systems Analysis > Basic MSA Templates > GLM GageRR (Expanded) Metrics to open the conversion template.
- Copy the Variance Component values in Sheet GLM1 - VarComp and paste the values into the yellow highlighted cells of the template as shown. For Gage Name, enter the information as shown. Use Standard Deviation Multiplier = 6.
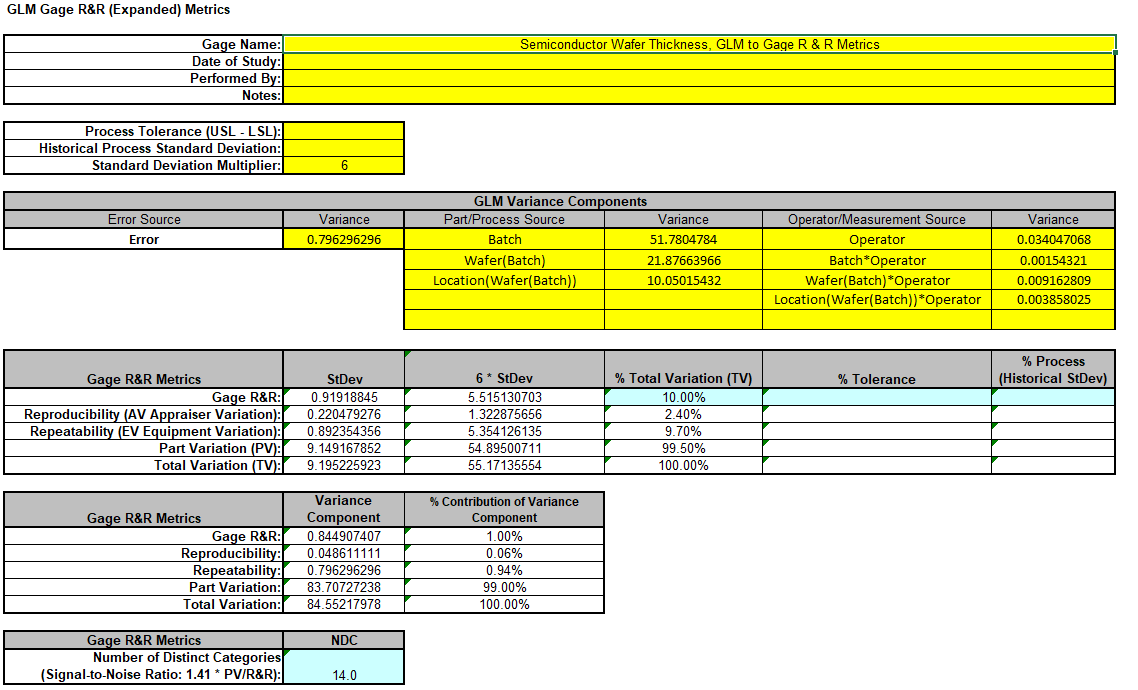
- This template converts the GLM Variance Components to Gage R&R metrics. With %Total Variation = 10%, this is an acceptable measurement system. The results match those given in the paper.
Example 8: Unbalanced Nested Factorial Experiment with Fixed and Random Factors
We will now analyze a nested factorial experiment adapted from Example 14.2 in Montgomery's Design and Analysis of Experiments book. The process is the hand insertion of electronic components on printed circuit boards and the goal
of the study is to improve the speed of the assembly operation. The design includes three assembly fixtures and two workplace layouts. Operators are required to perform the assembly.
In the book, four operators are randomly selected for each fixture-layout combination, but here we will use 4 operators for layout 1, but three for layout 2 making it an unbalanced design. The operators chosen for layout 1 are different
individuals from those chosen for layout 2, so operators are nested within layout. Because there are only three fixtures and two layouts, these are fixed factors but the operators are random factors, so this is a mixed model. The
treatment combinations in this design are run in random order, but the worksheet is shown in standard order. Two replicates are obtained. The assembly times are measured in seconds.
Since the design is unbalanced, SigmaXL will automatically use Restricted Maximum Likelihood (REML) to calculate variance components rather than the traditional ANOVA Expected Means Squares (EMS) method
Reference: Montgomery, D.C. (2020). Design and Analysis of Experiments, 10th Edition, John Wiley & Sons.
- Open the file Assembly Time Nested Factorial.xlsx. Click SigmaXL > Statistical Tools > General Linear Model > Fit General Linear Model. If necessary, click
Use Entire Data Table, click Next.
- Select Time, click Numeric Response (Y) >>, select Fixture and Layout, click Fixed Factors - Categorical (X) >>, select Operator, click Random Factors - Categorical (X) >>. Check
Nesting. For the left-side drop-down “Select a Factor or Covariate”, select Operator. For the right-side drop-down “Select a Factor to Nest in:“,
select (Layout). We will use the default Coding for Categorical Predictors (-1, 0, +1) and default Confidence Level = 95.0%. Check Main Effects Plots and Interaction Plots. Leave
Residual Plots, and Box-Cox Transformation
unchecked. Advanced Options are not available with Random Factors.
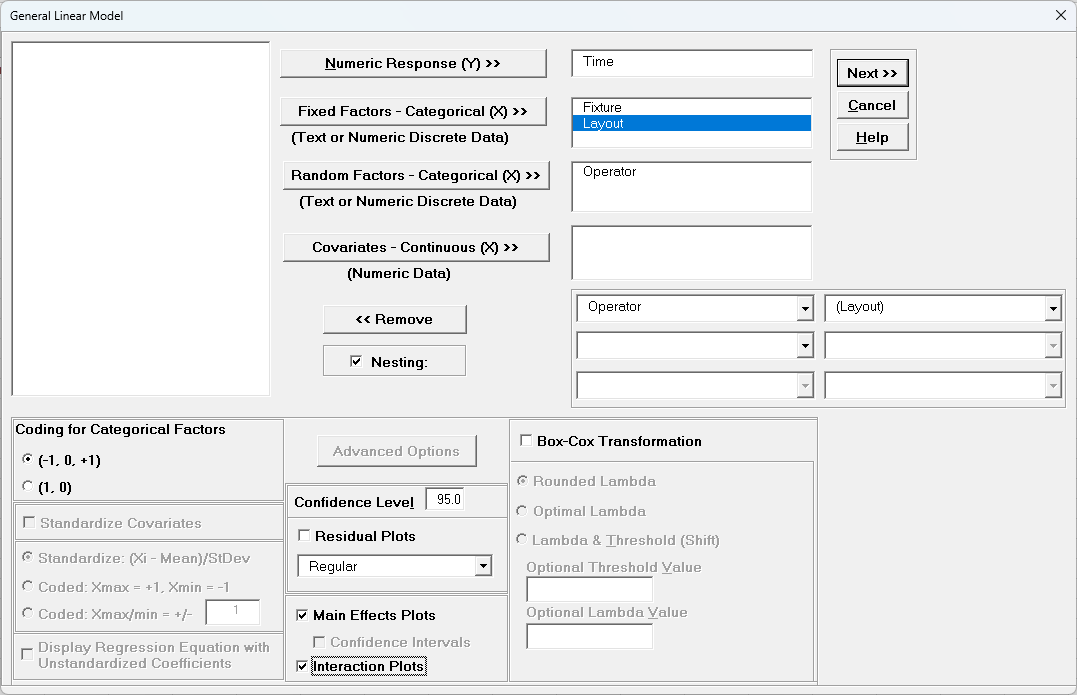
- Click Next >>.
- Using Term Generator, select ME + 2-Way Interactions. Click Select ALL >>.
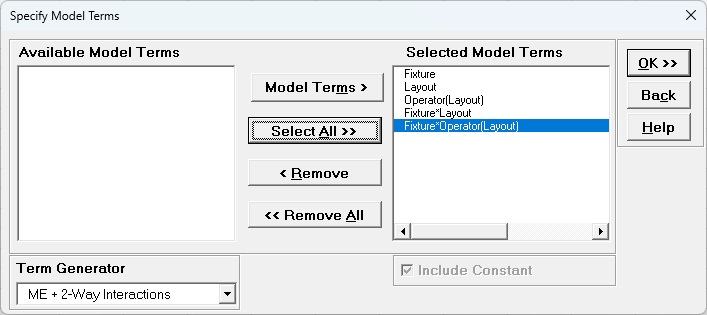
The term Operator(Layout) denotes that Operator is nested within Layout. Only legal 2-Way Interactions are available, so Operator*Layout is not available.
-
Click OK >>. The Variance Components report is given:
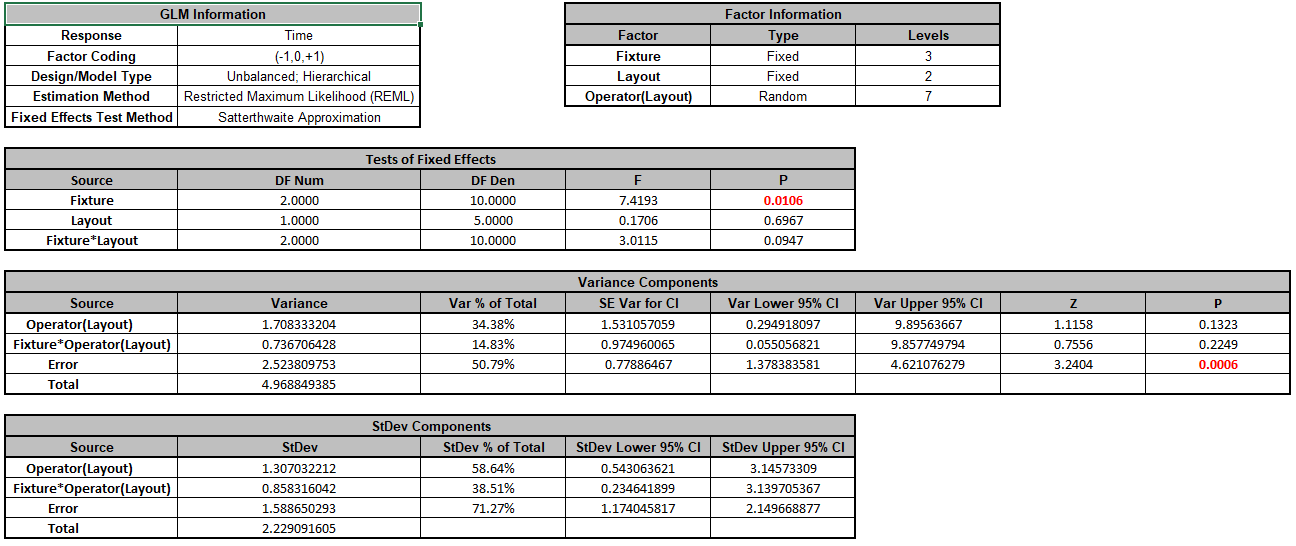
Since this is an unbalanced design, Restricted Maximum Likelihood (REML) is used to estimate the variance components. In Tests of Fixed Effects, we see that Fixture is significant but Layout and
Fixture*Layout are not significant. In Variance Components, Operator(Layout) contributes to 34.4% of the total variance and the interaction Fixture*Operator(Layout) contributes to
14.8% of the total variance. The P-Values for these variance components are not significant but this test is known to be underpowered when there are only a few levels (see Appendix Random Factors).
-
Click Sheet GLM1 - Plots to view the Main Effects and Interaction Plots.
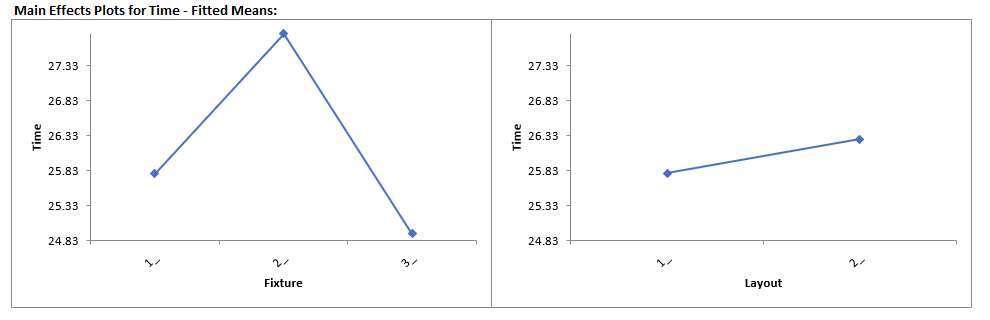
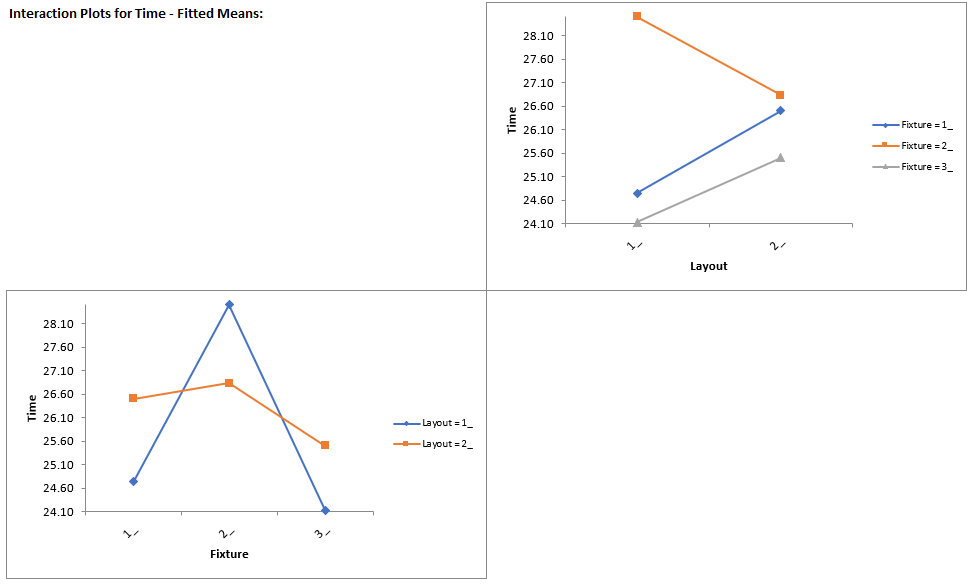
Clearly Fixture 2 results in an increase in assembly time. This may be an operator training issue but possibly the fixture can be modified to help the operators perform the assembly task more quickly.
Note: The Main Effects and Interaction Plots are computed from the predicted values of the regression model which assumes that all factors are fixed. Confidence Intervals for the Main Effects plots are not available when there
is a Random Factor.