DiscoverSim™ Case Studies

Case Study 1 – Basic Profit Simulation: Introduction

This is an example of DiscoverSim Monte Carlo simulation to determine probability of daily profit using a basic profit model for a small retail business. We will apply distribution fitting to historical data and specify input correlations to define the model in a way that closely matches our real world business.

Profit Simulation with DiscoverSim

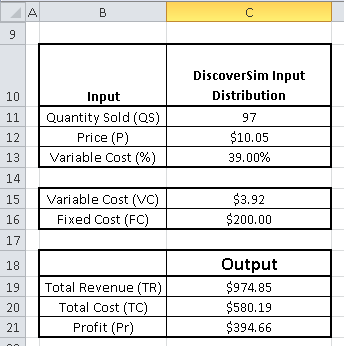
1. Open the workbook Profit Simulation. DiscoverSim Input Distributions will simulate the variability in Quantity Sold, Price and Variable Cost. We will use distribution fitting with historical data to determine which distributions to use and what parameter values to enter. Input Distributions will then be specified in cells C11, C12 and C13. The output, Profit, will be specified at cell C21 using the formula given above.
   
   


2. Select the Historical_Data sheet. This gives historical data for Quantity Sold, Price and Variable Cost.
   
   
   
   Tip: At this point use the SigmaXL tool (bundled with DiscoverSim) to obtain descriptive statistics to test for normality (SigmaXL > Statistical Tools > Descriptive Statistics). Quantity Sold has an Anderson Darling Normality test p-value = 0.83, so may be considered as a Normal Distribution, but since it is a count we will apply DiscoverSim’s distribution fitting using discrete distributions. Price and Variable Cost are non-normal with AD p-values less than .05, so we will use DiscoverSim’s distribution fitting for continuous data. SigmaXL’s correlation matrix should also be used to evaluate correlations (SigmaXL > Statistical Tools > Correlation Matrix). The Spearman Rank correlation for Quantity Sold versus Price is -0.8 (Note: DiscoverSim uses the more robust Spearman Rank correlation rather than Pearson’s correlation). SigmaXL’s graphical tools such as Histograms and Scatterplots should also be used to view the historical data.


3. Select DiscoverSim > Distribution Fitting > Batch Distribution Fit:
   
   
4. The data range has been preselected and appears in the dialog. Note: if a different range is required, click on to change it or select Use Entire Data Table to automatically select the data.
   
   


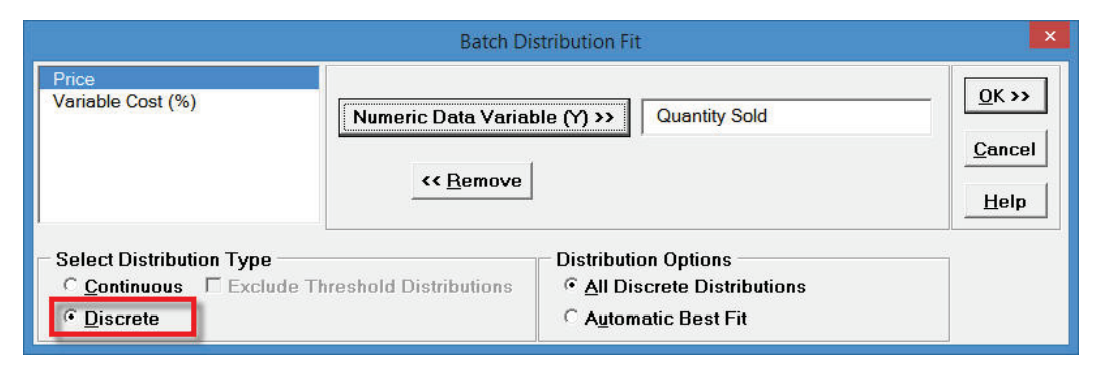
5. Click Next. Since Quantity Sold is count data, i.e. a discrete variable, select Discrete. Select Quantity Sold as the Numeric Data Variable (Y). For Distribution Options use the default All Discrete Distributions as shown:
   
   


6. Click OK. The resulting discrete distribution report is shown below:
   
   
   
   

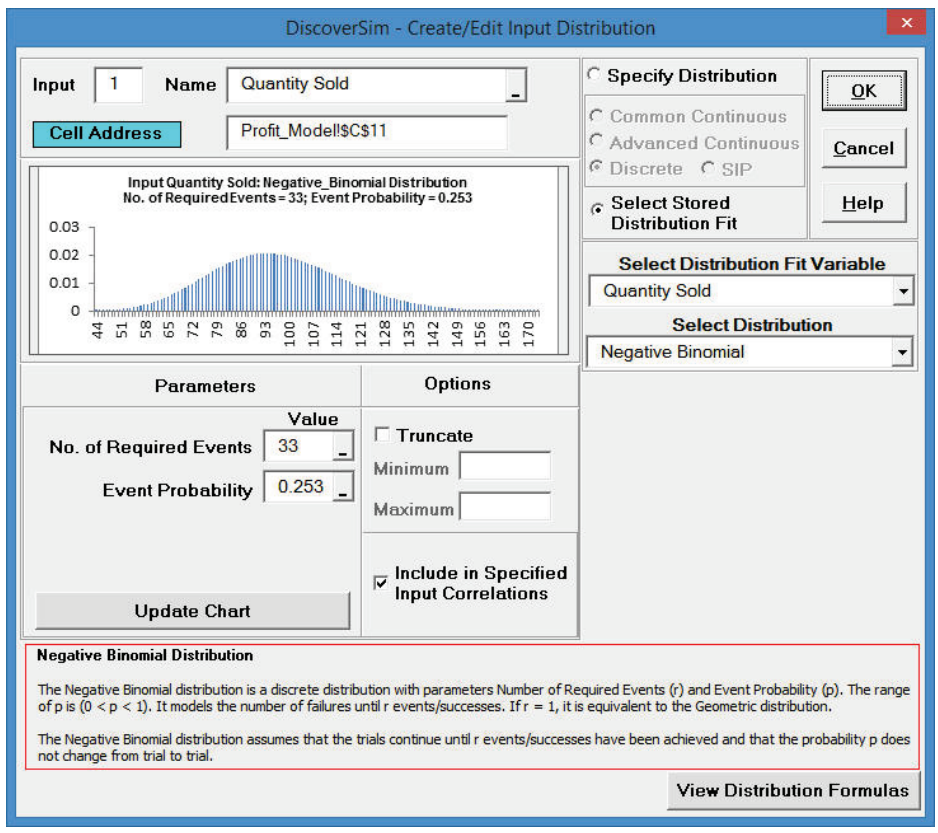
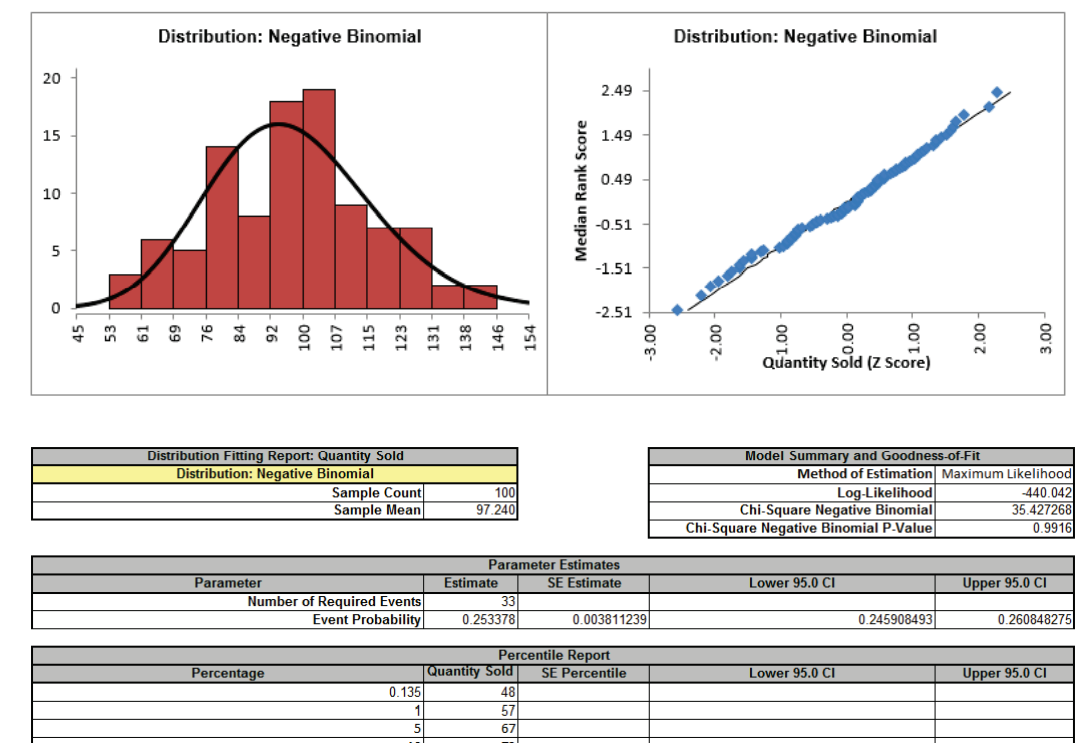
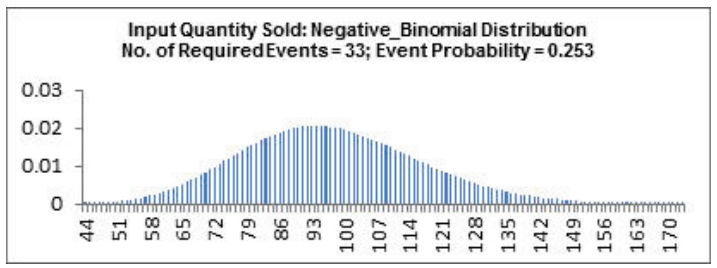
   Since these are discrete distributions, Chi-Square is the statistic used to determine goodness-of-fit. The distributions are sorted by Chi-Square in ascending order. The best fit distribution is Negative Binomial with Chi-Square = 35.4 and p-value = 0.99. The parameters are Number of Required Events = 33 and Event Probability = 0.2534.

   
   

   Tip: If the best fit discrete distribution has a p-value less than  .05 indicating a poor goodness-of-fit, none of the discrete distributions are adequate for use in Monte-Carlo simulation. In this case you should redo the distribution fit using the Continuous option (Note that you can use the continuous option for discrete data, but you cannot use discrete distributions for continuous data). After creating a DiscoverSim input distribution with the best fit (or normal if applicable), use Excel’s ROUND(number, 0) function to obtain integer values from the continuous distribution.



7. Now we will apply distribution fitting to Price and Variable Cost. Select the Historical_Data sheet and repeat the above steps. Both variables are continuous so use the default Select Distribution Type Continuous. The resulting distribution reports are shown below.
   
   
   
   


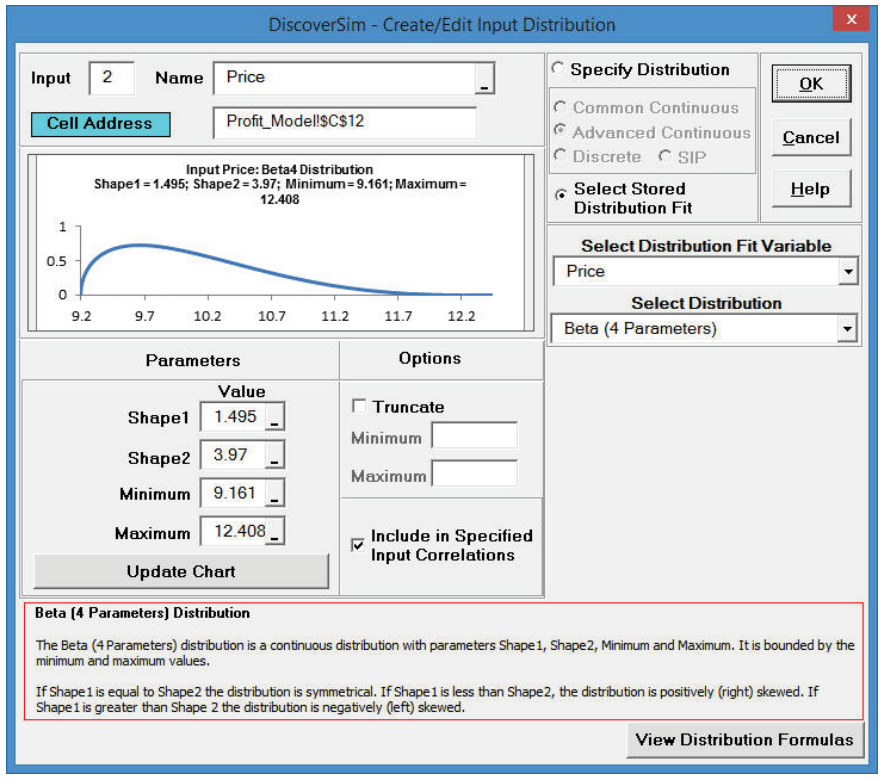
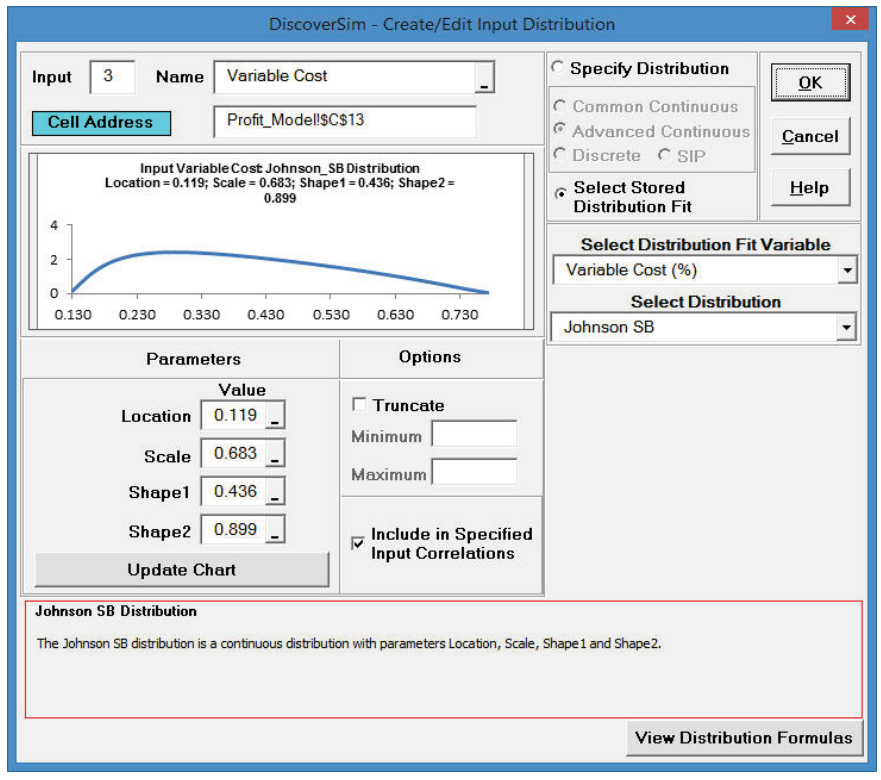
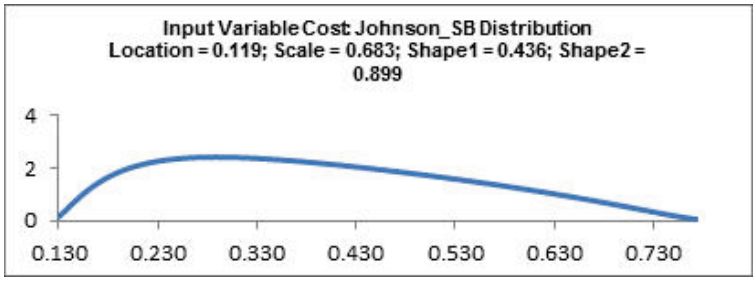
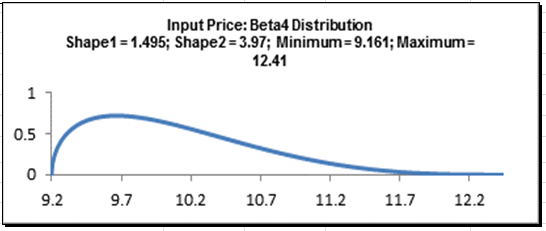
8. DiscoverSim uses the Anderson Darling statistic to determine goodness-of-fit for continuous distributions. The distributions are sorted by the AD statistic in ascending order. The best fit distribution for Price is Beta (4 Parameters) with AD Stat = .34 and AD p-value = 0.47. The best fit distribution for Variable Cost (%) is Johnson SB with AD Stat = .31 and AD p-value = 0.41


9. Optional Specified Distribution Fit analysis: This is a detailed view of the distribution fit for a specified distribution with:
   
   
   • • Histogram and Probability Plot.
   • • Parameter estimates, standard errors (SE Estimate) and confidence intervals for parameter estimates.
   • • Percentile Report with the following: 0.135, 1, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 99, 99.865.
   • o Note that percentiles are computed using the distribution and estimated parameters, not empirical data.
   • • Standard errors and confidence intervals for the percentile values
   • • Model Summary and Goodness-of-Fit statistics.
   
   Select DiscoverSim > Distribution Fitting > Specified Distribution Fit:
   
   
   
   

   Using the default settings as shown, click OK. This produces a detailed distribution fit report for Quantity Sold using the Negative Binomial distribution:

   
   


10. Now we will apply specified distribution fitting to Price and Variable Cost. Repeat the above steps using the default best fit distributions to produce a detailed distribution fit report:
    
    
    
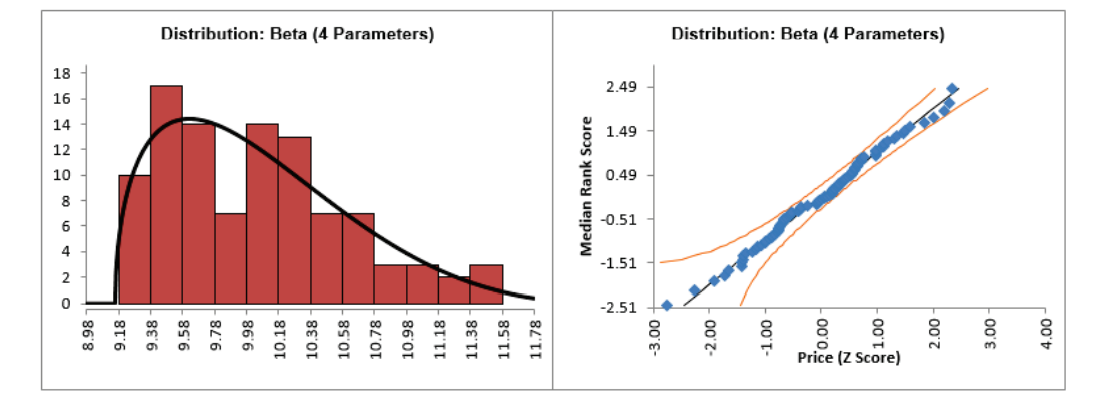
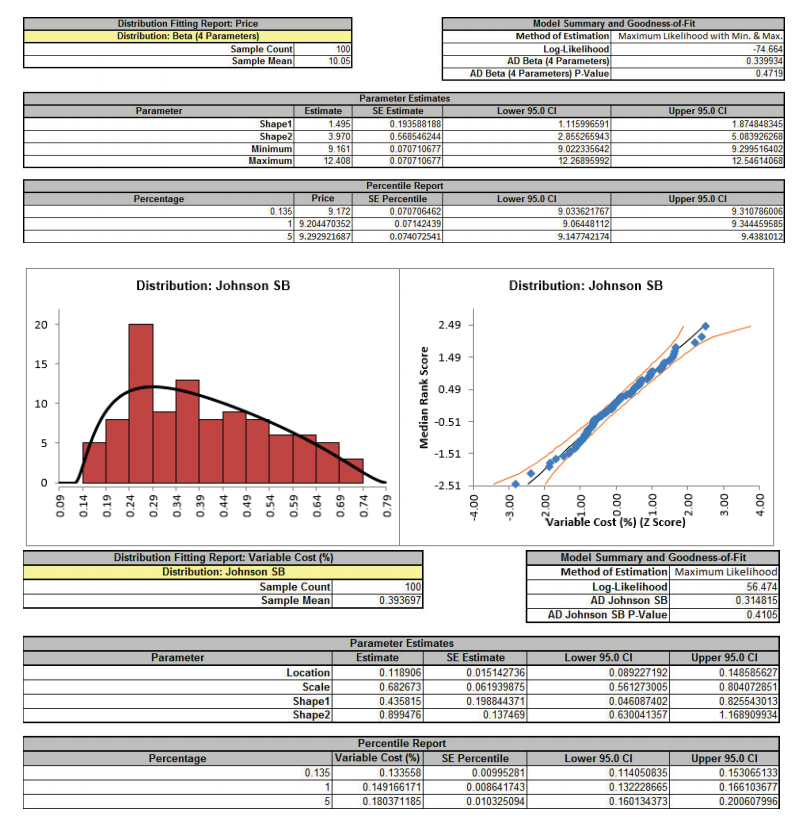
11. The detailed distribution analysis clearly shows that we have a good fit for all 3 variables. Now we will use the stored distribution fits to create a DiscoverSim model.


12. Select Profit_Model sheet. Click on cell C11 to specify the Input Distribution for Quantity Sold. Select DiscoverSim > Input Distribution.


13. Click Select Stored Distribution Fit. We will use the default variable Quantity Sold for Select Distribution Fit Variable and Negative Binomial for Select Distribution. The parameter values for Number of Required Events and Event Probability are automatically populated from the distribution fit results for Quantity Sold.


14. Enter “QuantitySold” as the Input Name.


15. Click Update Chart. The completed Create/Edit Input Distribution dialog is shown below:
    
    


16. Click OK. Hover the cursor on cell C11 in the Profit_Model sheet to view the DiscoverSim graphical comment showing the distribution and parameter values:
    
    


17. Click on cell C12 to specify the Input Distribution for Price. Select DiscoverSim > Input Distribution.


18. Click Select Stored Distribution Fit. Select the variable Price for Select Distribution Fit Variable and the default Beta (4 Parameters) for Select Distribution. The parameter values for this distribution are automatically populated from the distribution fit results for Price.


19. Enter “Price” as the Input Name.


20. Click Update Chart. The completed Create/Edit Input Distribution dialog is shown below:
    
    


21. Click OK. Hover the cursor on cell C12 in the Profit_Model sheet to view the DiscoverSim graphical comment showing the distribution and parameter values:
    
    


22. Click on cell C13 to specify the Input Distribution for Variable Cost. Select DiscoverSim > Input Distribution.


23. Click Select Stored Distribution Fit. Select Variable Cost for Select Distribution Fit Variable and the default Johnson SB for Select Distribution. The parameter values for this distribution are automatically populated from the distribution fit results for Variable Cost.


24. Enter “Variable Cost” as the Input Name.


25. Click Update Chart. The completed Create/Edit Input Distribution dialog is shown below:
    
    


26. Click OK. Hover the cursor on cell C13 in the Profit_Model sheet to view the DiscoverSim graphical comment showing the distribution and parameter values:
    
    


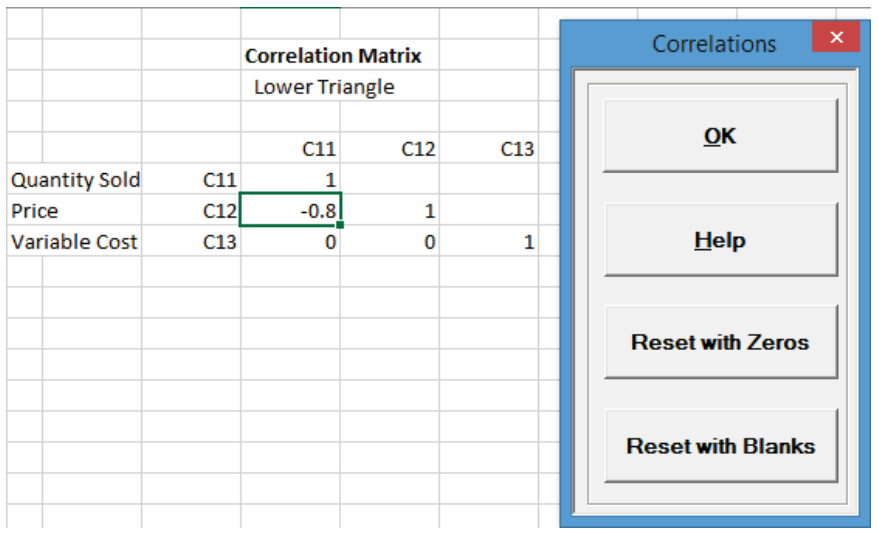
27. Now we will specify the correlation between the inputs Quantity Sold and Price. Select DiscoverSim > Correlations:
    
    


28. As discussed above, the Spearman Rank correlation between Quantity and Price is -.8. This negative correlation is expected: as order quantity increases, unit price decreases. Enter the value -.8 in the column Price, row Quantity and press Enter.
    
    
    
    Tips: It is not necessary to enter a correlation value in the upper triangle. The lower triangle specifies the correlations so any value entered in the upper will be ignored. The diagonal of 1’s should not be altered. Reset with Zeros clears any specified correlations in the lower triangle and replaces them with zeros. Reset with Blanks clears any correlations in the lower triangle and replaces them with blanks. This is useful if you wish to then specify correlations between inputs without the constraint of requiring independence on the other inputs.
    
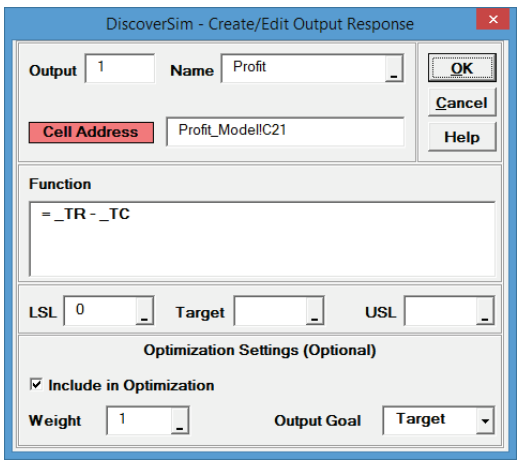
    Click OK.


29. Now we will specify the Profit model output. Click on cell C21. Select DiscoverSim > Output Response:
    
    


30. Enter the output Name as “Profit”. Enter the Lower Specification Limit (LSL) as 0. The Include in Optomization, Weight and Output Goal settings are used only for multiple response optimization, so do not need to be modified in this example.
    
    
    
    Click OK.


31. Hover the cursor on cell C21 to view the DiscoverSim Output information.
    
    


32. Select DiscoverSim > Run Simulation:
    
    


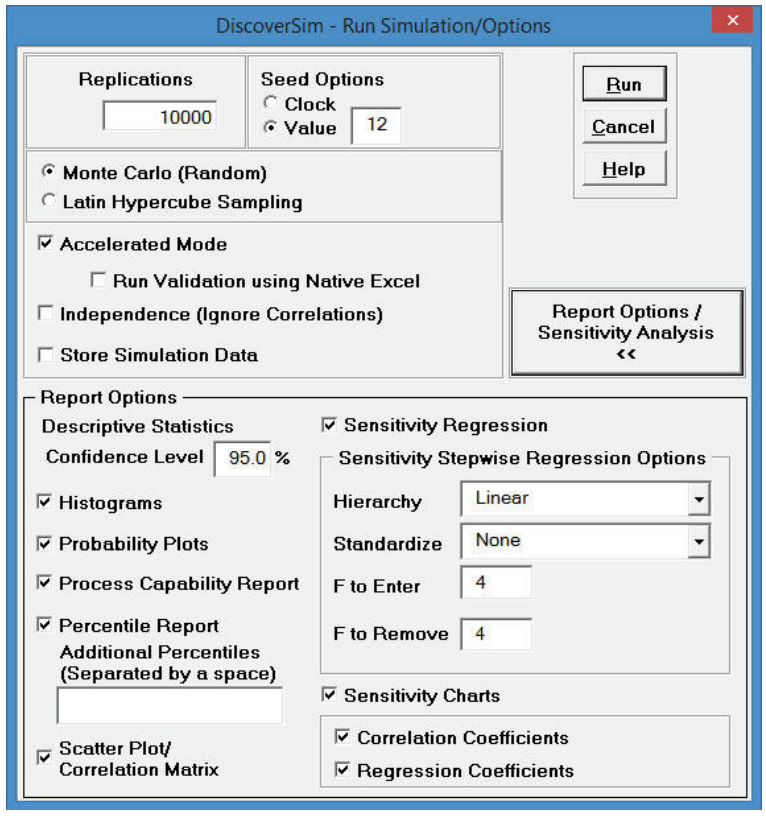
33. Click Report Options/Sensitivity Analysis. Check Percentile Report, Scatter Plot/Correlation Matrix, Sensitivity Regression Analysis, Sensitivity Charts - Correlation Coefficients and Regression Coefficients. Select Seed Value and enter “12” as shown, in order to replicate the simulation results given below (note that 64 bit DiscoverSim will show slightly different results).
    
    
    
    Click Run


34. The DiscoverSim Output Report shows a histogram, normal probability plot, descriptive statistics, process capability indices, a percentile report and a percentile process capability report:
    
    
    
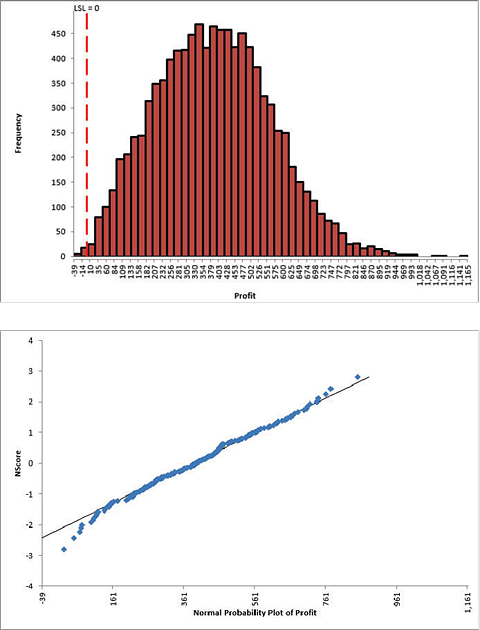
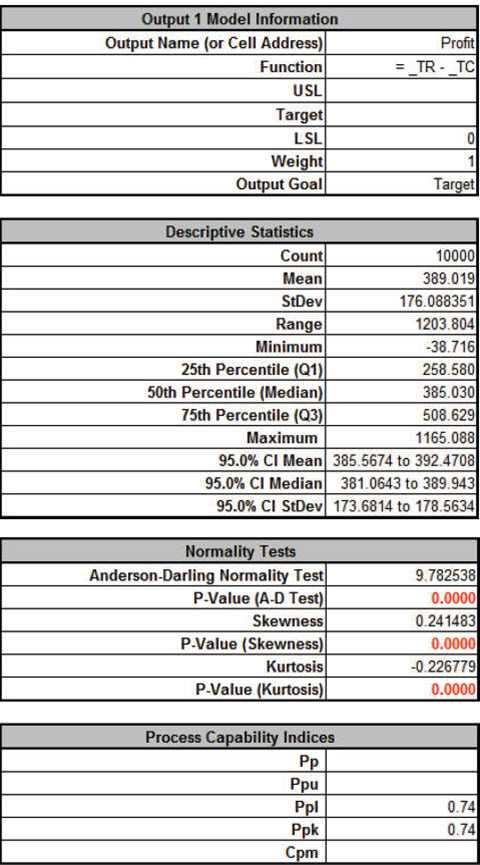
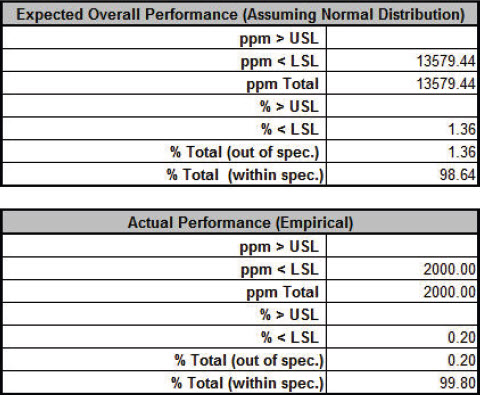
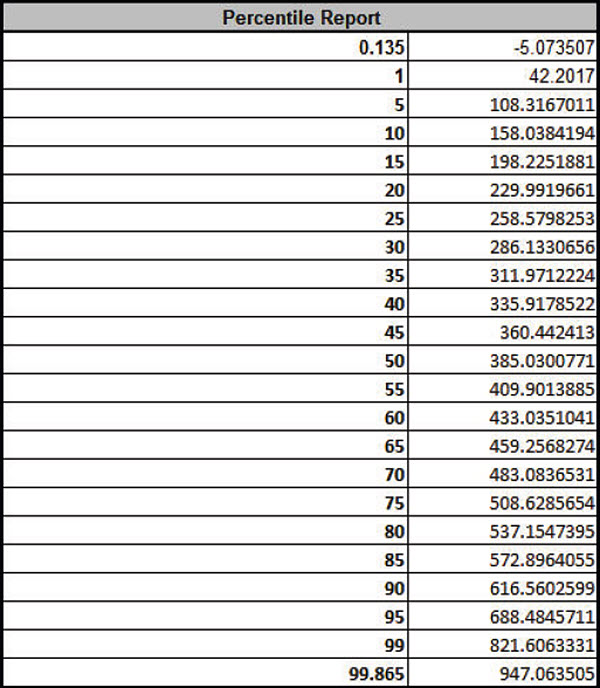
    From the histogram and detailed report we see that typically we should expect a positive daily profit, but the variation is large. The likelihood of profit loss is approximately 0.20% (see Actual Performance (Empirical): %Total (out of spec). Note that the “expected” loss of 1.36% assumes a normal distribution, so that is not applicable here because the output distribution is not normal (Anderson-Darling p-value is much less than .05).
    
    Note: If Seed is set to Clock, there will be slight differences in the reported values with every simulation run due to a different starting seed value derived from the system clock.
    
    Tip: Percentile Process Capability Indices for non-normal data can be calculated from the Percentile Report as follows:
    
    Percentile Pp = (USL – LSL)/( 99.865 percentile – 0.135 percentile)
    
    Percentile Ppu = (USL – 50th percentile)/(99.865 percentile – 50th percentile)
    
    Percentile Ppl = (50th percentile – LSL)/(50th percentile – 0.135 percentile)
    
    Percentile Ppk = min(Ppu, Ppl)
    
    Since we only have a lower specification limit (LSL = 0), Percentile Ppl is calculated as: Percentile Ppl = (385.03 - 0) / (385.33 - (-5.07)) = 0.99


35. Optional Nonnormal Process Capability Analysis: DiscoverSim Version 2.1 now includes Nonnormal Process Capability with Distribution Fitting. To utilize this stand-alone feature for the Profit data, perform the following steps:
    
    
    • • Click Run Simulation, select Store Simulation Data, click Run.
    
    
    • • Select DSim Data sheet, select Profit column (D1:D10001).
    
    
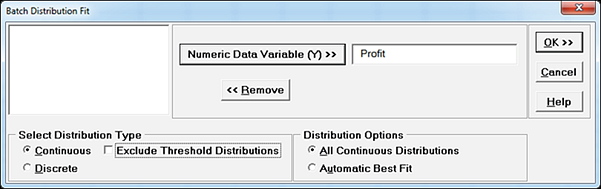
    • • Select Distribution Fitting > Batch Distribution Fit, click Next, select Profit, uncheck Exclude Threshold Distributions:
    
    
    
    
    • • Click OK. The batch fit will take approximately 1-2 minutes due to the large dataset and inclusion of Threshold distributions.
    
    
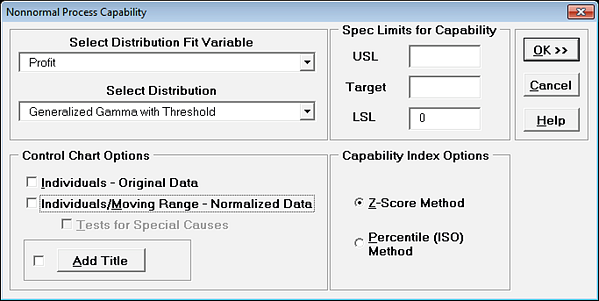
    • • The best fit distribution is Generalized Gamma with Threshold. Unfortunately, it is not a good fit to the data with the AD P-Value < .001, but we will proceed for demonstration purposes. Select Distribution Fitting > Nonnormal Process Capability.
    
    
    • • Select Profit. Enter LSL = 0. The best fit distribution is selected as Generalized Gamma with Threshold. Uncheck Control Chart Options.
    
    
    
    
    • • Click OK. The Ppk using Generalized Gamma is 0.95 which, even though a poor fit, is closer to the above Percentile Ppk value of 0.99 than the normal distribution Ppk of .74.
    
    
36. Click on the Scatter Plot Matrix sheet to view the Input-Output relationships graphically:
    
    
    
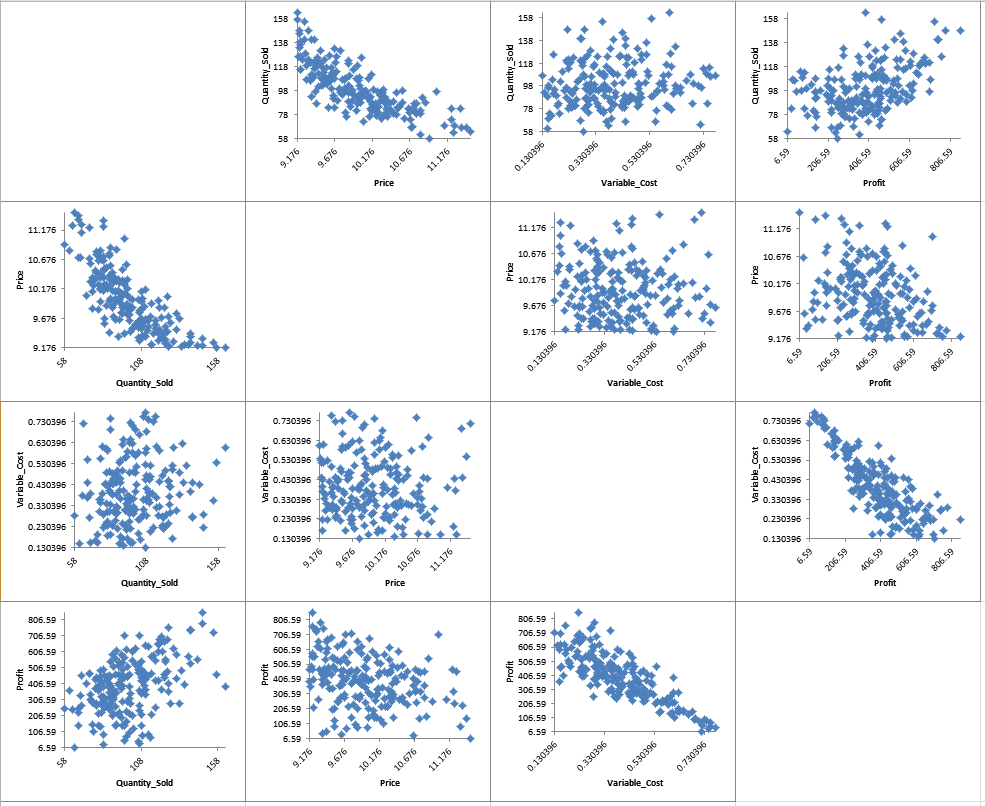
    Here we see the negative correlation that was specified between the inputs “Price” and “Quantity Sold”, as well as the strong negative correlation between “Variable Cost” and “Profit”.


37. Click on the Correlation Matrix sheet to view the Input-Output correlations numerically:
    
    


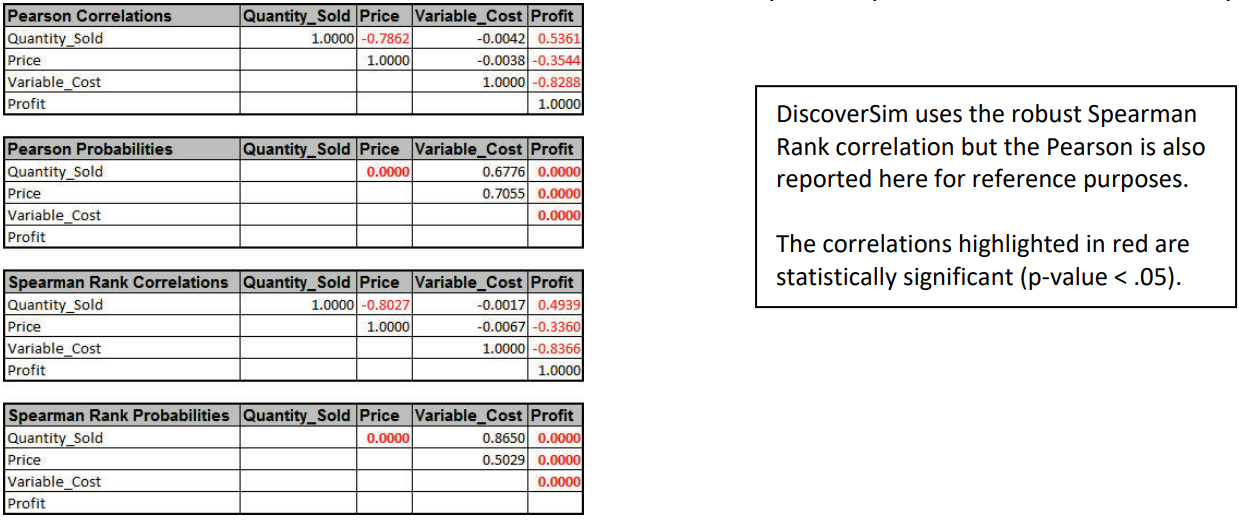
38. In order to increase profit (and reduce the variation), we need to understand what is driving profit, i.e., the key “X” factor. To do this we will look at the sensitivity charts. Click on the Sensitivity Chart sheet:
    
    
    
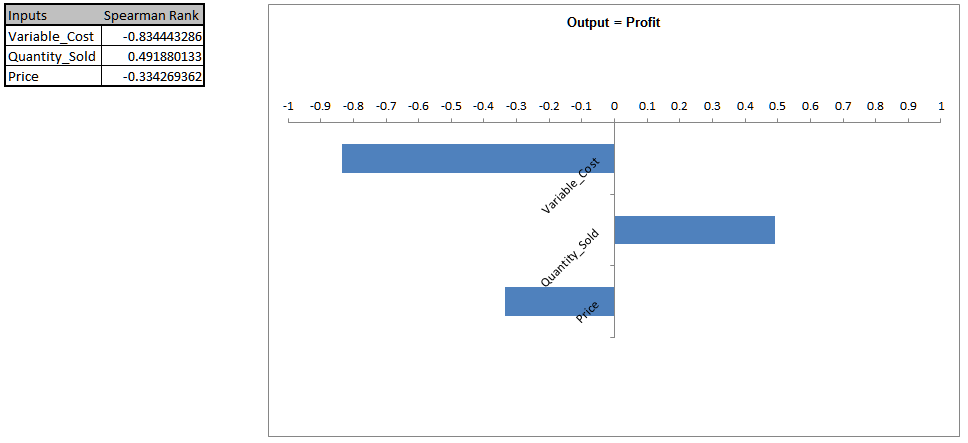
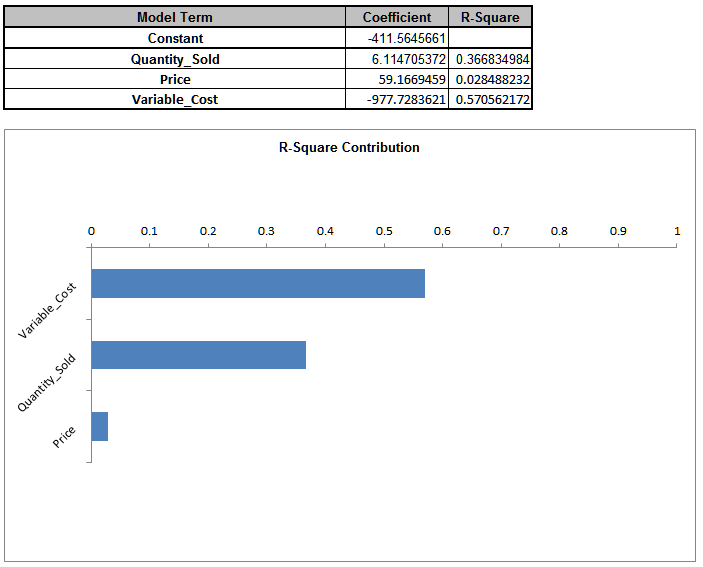
    Here we see that “Variable Cost” is the dominant input factor affecting “Profit” with a negative correlation (lower variable cost means higher profit). The next step would then be to find ways to minimize the variable cost (and reduce the variation of variable cost). “Quantity Sold” is the second important input factor. It is interesting to note that “Price” is the least important factor in this Profit simulation model.


39. To view R-Squared percent contribution to variation, click on the Sensitivity Regression sheet:
    
    


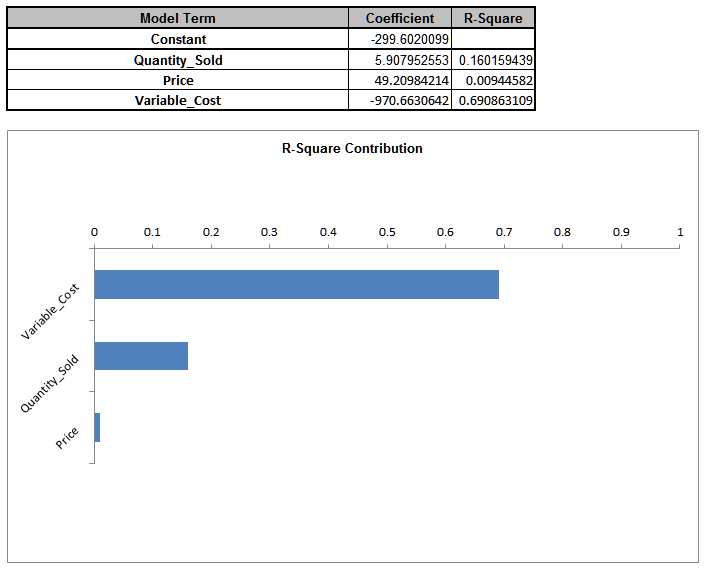
40. When strong correlations are present in the inputs, Sensitivity Correlation Analysis and Sensitivity Regression Analysis may be misleading, so it is recommended that the simulation be rerun with Independence (Ignore Correlations) checked to validate the sensitivity results:
    
    
    
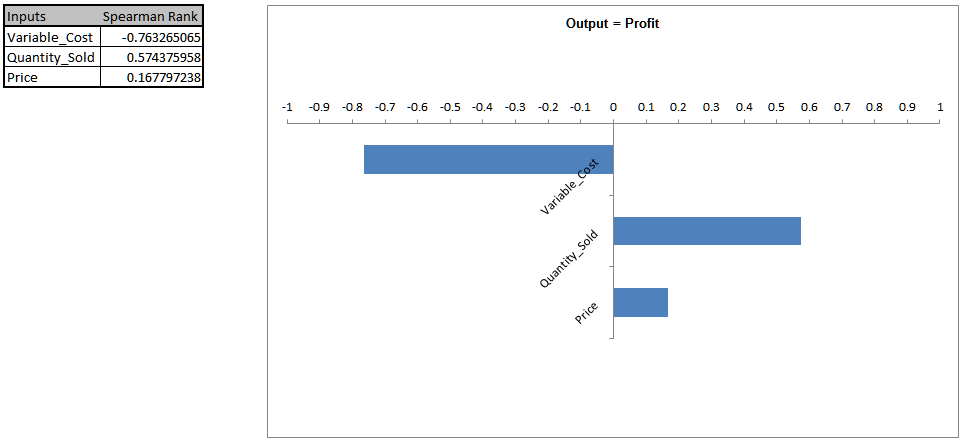
    In this case the input factor prioritization remains the same, but “Price” shows a small positive correlation rather than negative.


41. The revised R-Square Percent Contribution report is shown below: