Design of Experiments
- Home /
- DOE Catapult

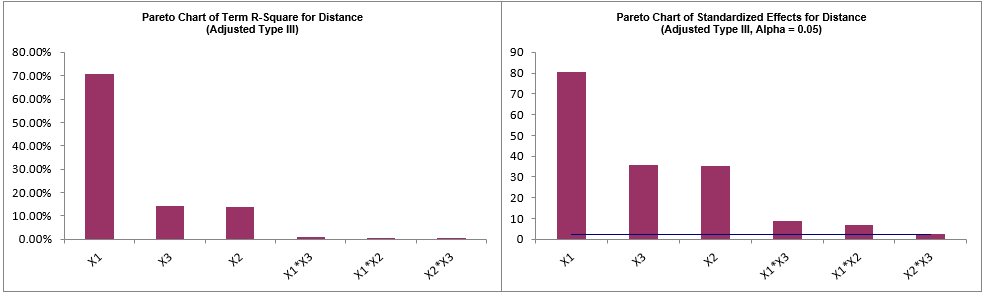
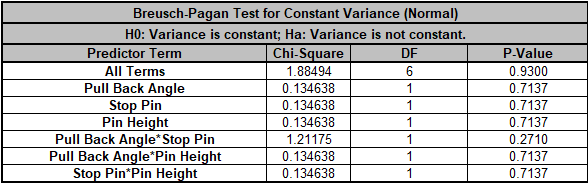
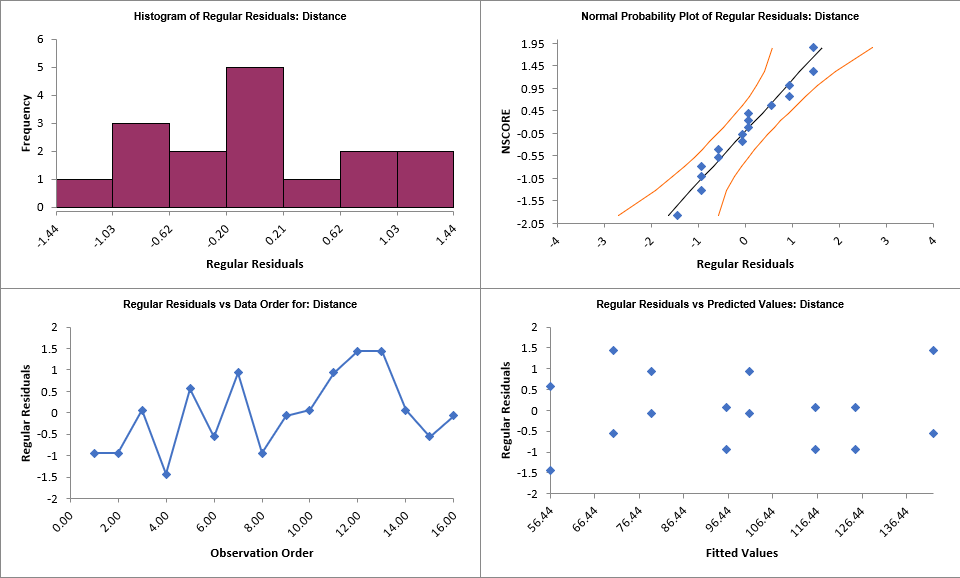
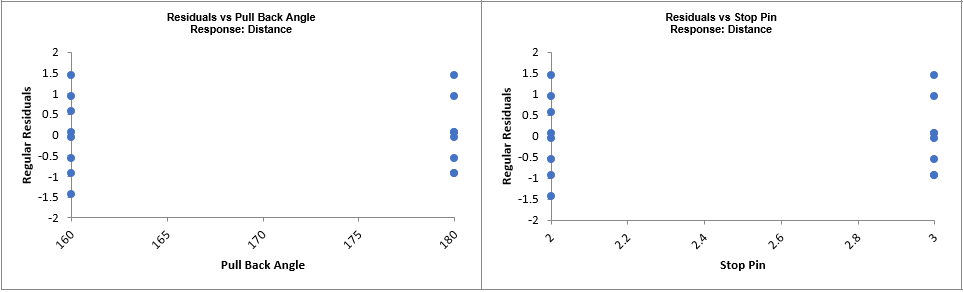
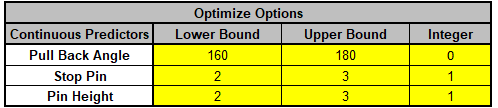
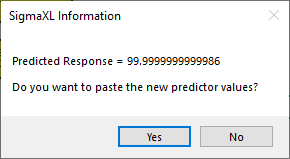
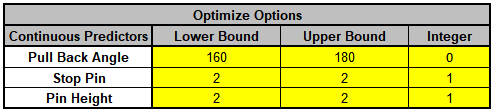
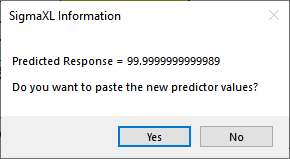
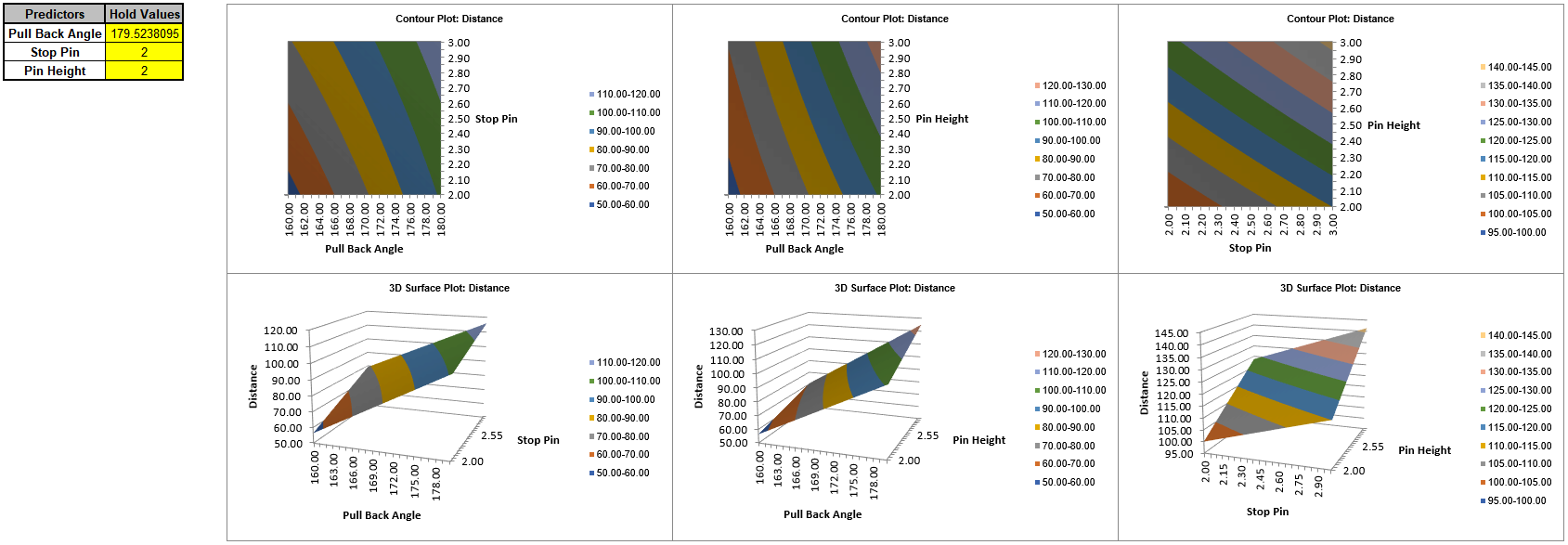
Catapults are frequently used in Six-Sigma or Design of Experiments training. They are a powerful teaching tool and make the learning fun. If you have access to a catapult, we recommend that you perform the actual experiment and use your own data. Of course, you can also follow along using the data provided. The response variable (Y) is distance, with the goal being to consistently hit a target of 100 inches.

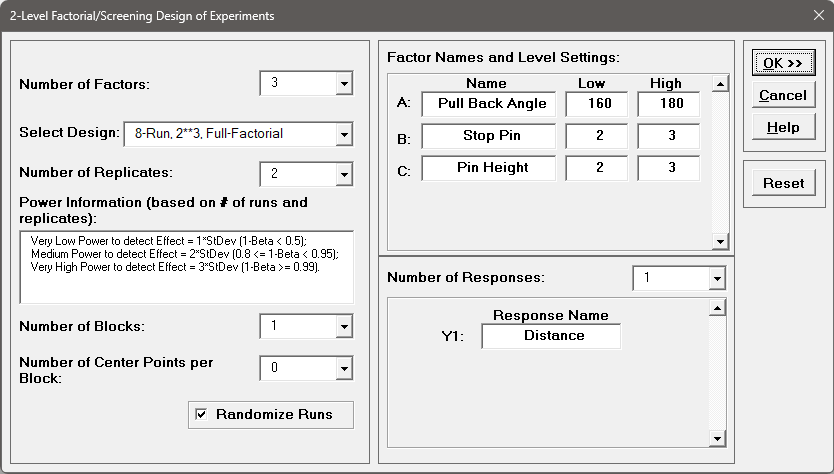
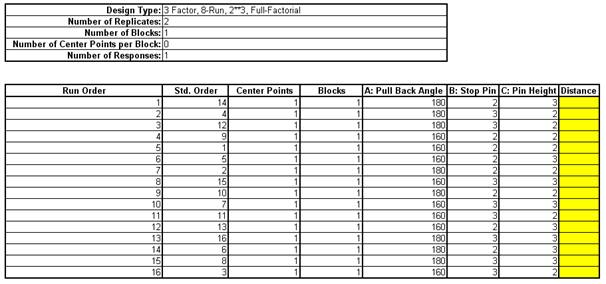
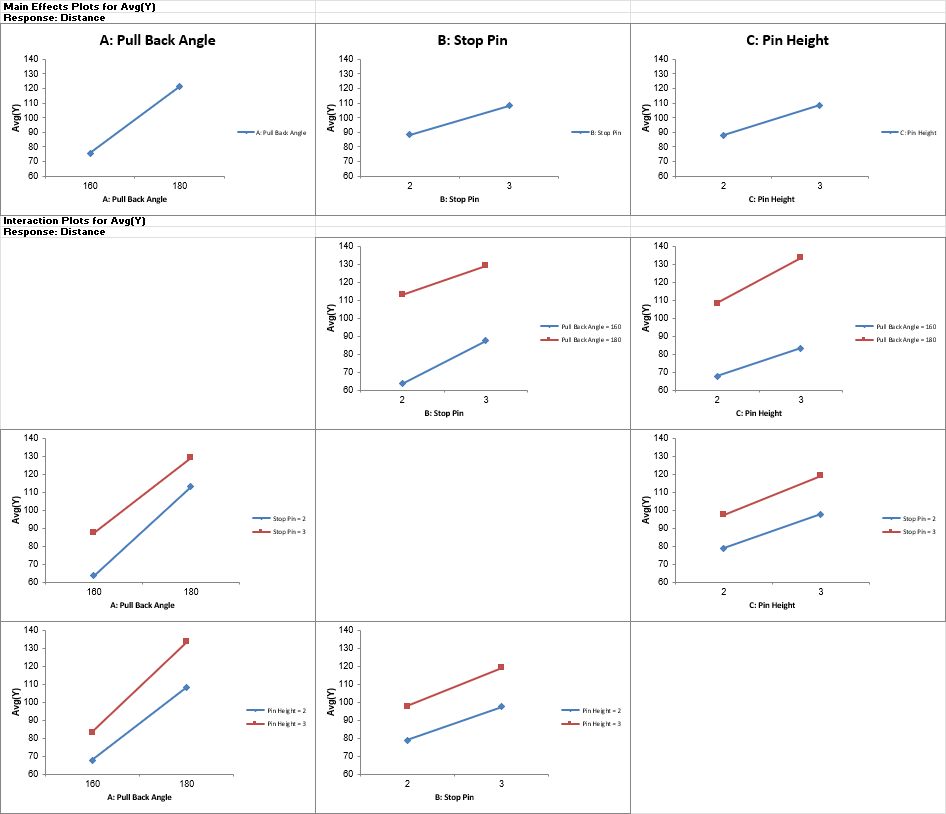
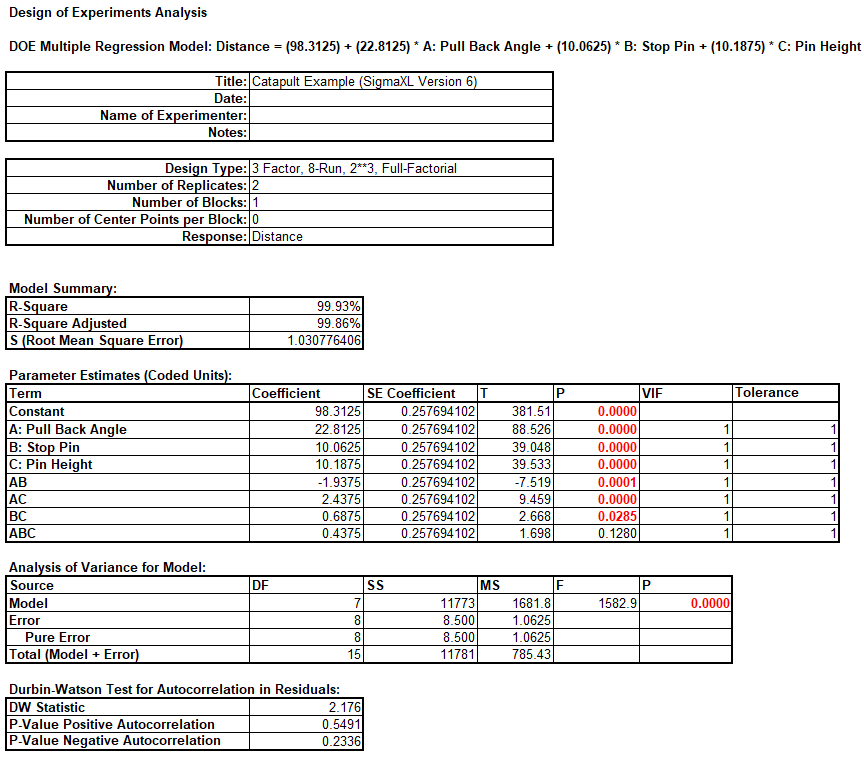
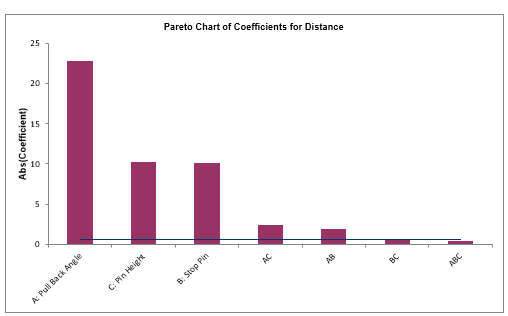
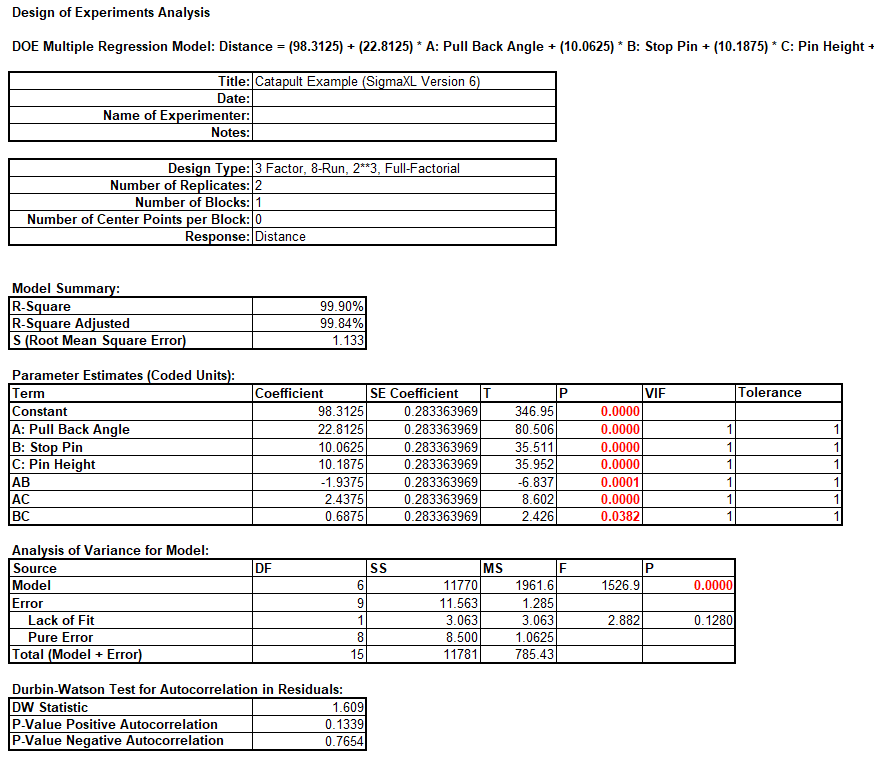
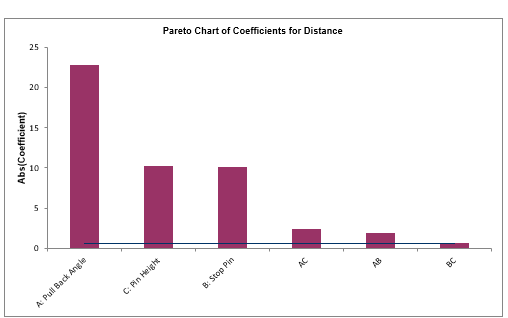
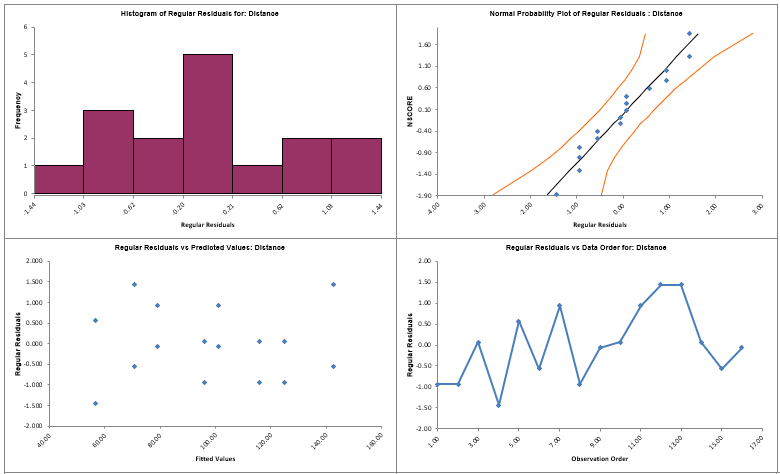

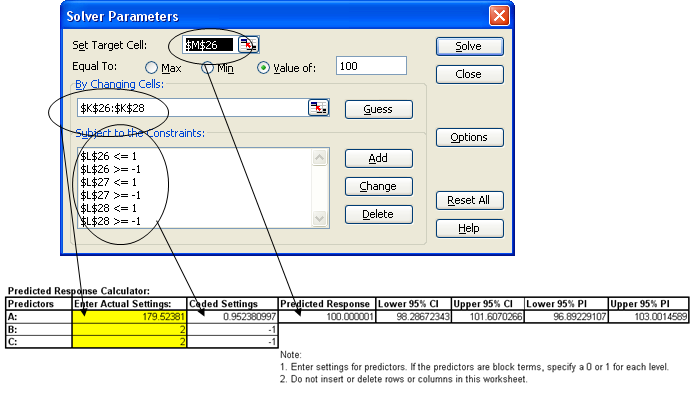
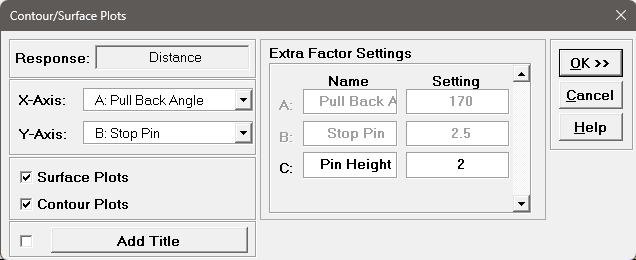
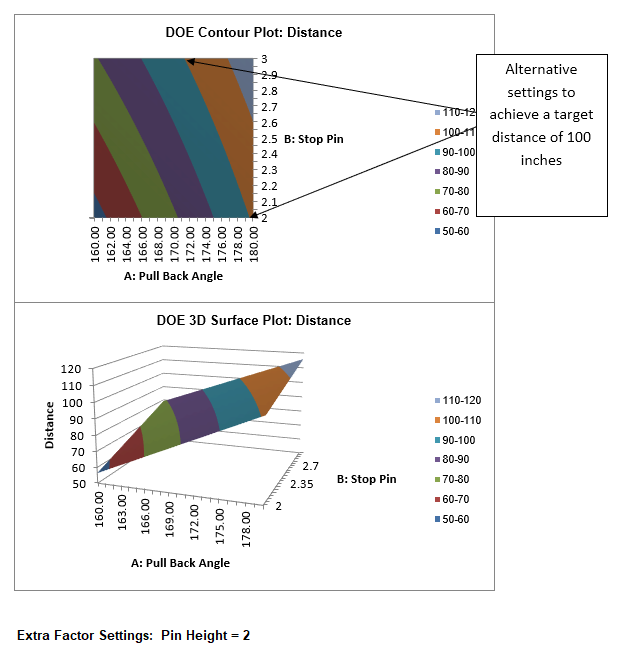
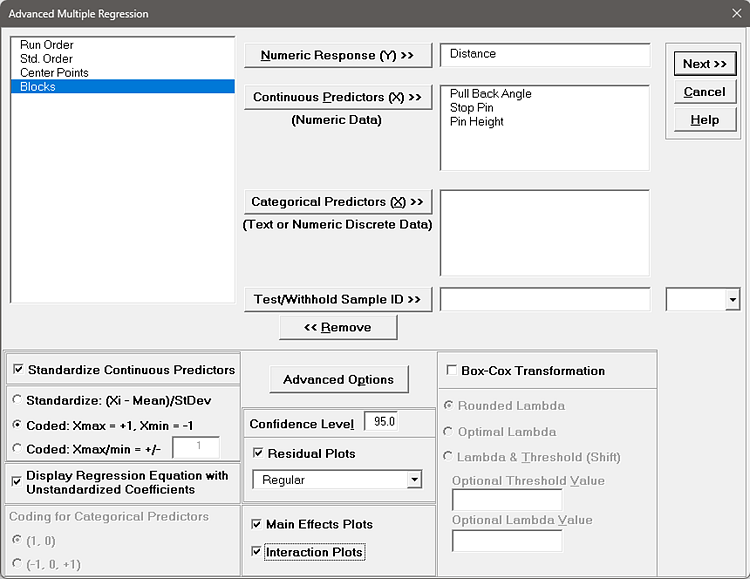
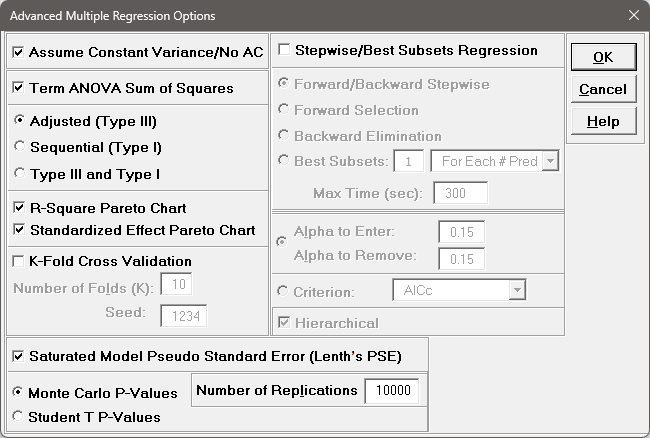
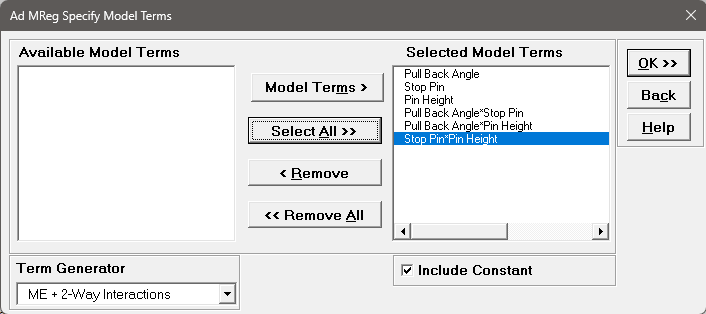
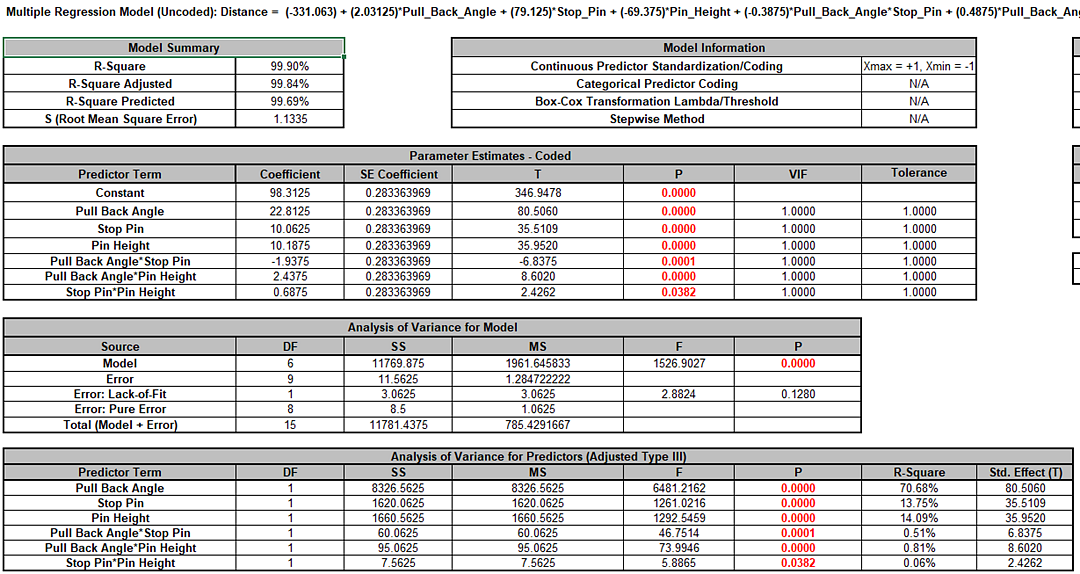
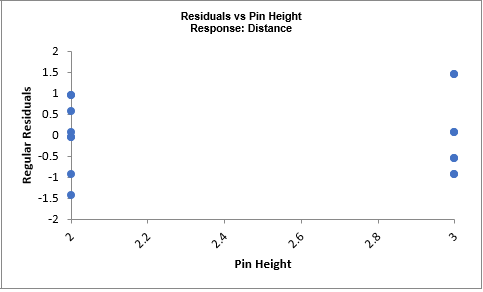
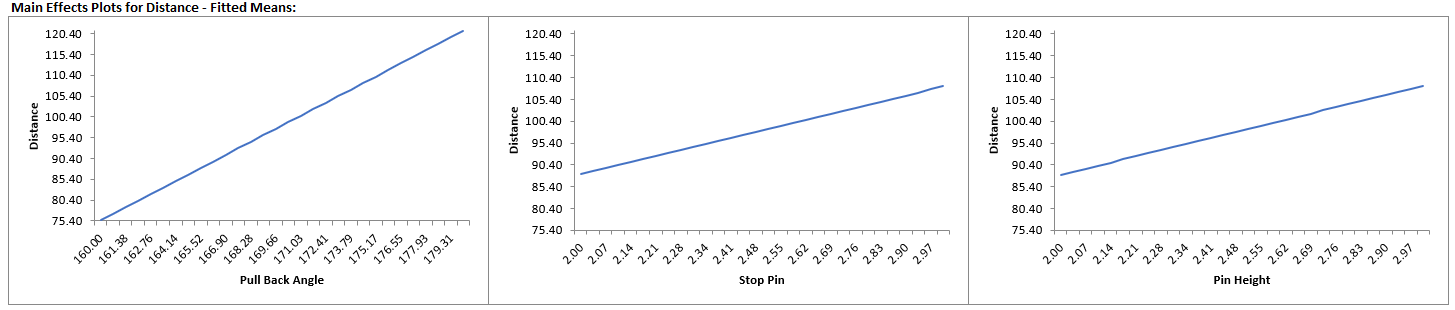
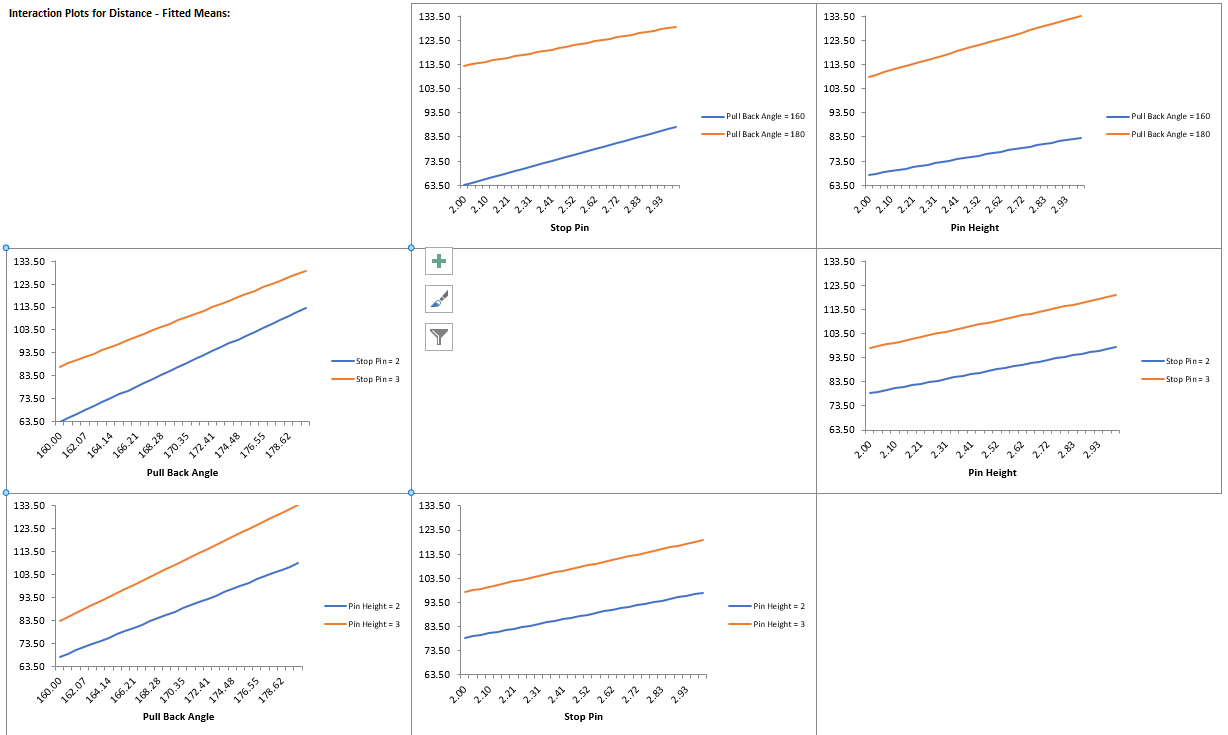
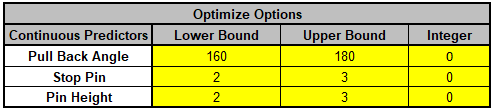
We will now redo the above analysis and optimization using Advanced Multiple Regression.