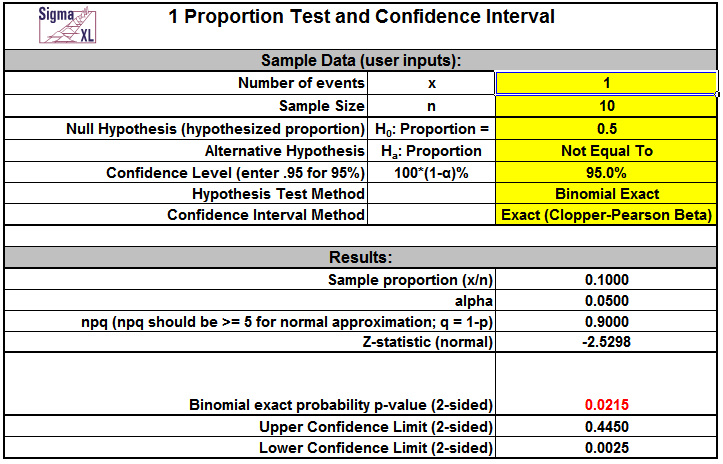
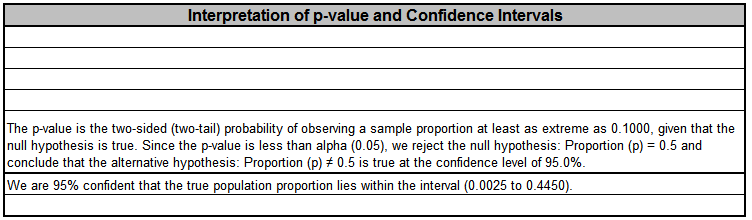
1. Enter summarized Sample Data, Null Hypothesis and Confidence Level in cells with yellow highlight. Do not modify any other part of this worksheet.
2. Select Alternative Hypothesis and Methods using drop-down. If x = 0, it is recommended that the Alternative Hypothesis be set to one-sided "Less Than." If x = n, set the Alternative Hypothesis to one-sided "Greater Than."
3. Hypothesis Test Method:
• Binomial Exact is recommended.
• Use Normal Approximation only when n is large and proportion is close to 0.5 (check that np >= 5 and nq >= 5, or the more conservative npq, shown above, >= 5). See Rosner (2010).
4. Confidence Interval Method (recommendations based on literature review, see references below):
• Confidence intervals for binomial proportions have an "oscillation" phenomenon where the coverage probability varies with n and p.
• Exact (Clopper-Pearson) is strictly conservative and will guarantee the specified confidence level as a minimum coverage probability, but results in wide intervals. Recommended only for applications requiring strictly conservative intervals.
• Wilson Score and Jeffreys Beta have mean coverage probability matching the specified confidence interval. We recommend Wilson for two-sided confidence intervals and Jeffreys for one-sided.
• Normal Approximation (Wald) is not recommended, but included here to validate hand calculations. Use only when n is large and proportion is close to 0.5 (check that npq, shown above, >= 5).
5. This calculator will automatically detect the version of Excel and use the appropriate statistical functions.

References:

Agresti, A. and Coull, B.A.(1998), Approximate is Better than “Exact” for Interval Estimation of Binomial Proportions. The American Statistician,52,119–126.

Brown, L. D., Cai, T. T. and DasGupta, A. (2001), Interval estimation for a binomial proportion. Statistical Science, 16, 101-133. With comments and a rejoinder by the authors.

Cai, T. T. (2005), One-sided confidence intervals in discrete distributions. J. Statist. Plann. Inference,131, 63-88.

Clopper, C.J.,and Pearson, E.S.(1934), The Use of Confidence or Fiducial Limits Illustrated in the Case of the Binomial. Biometrika, 26, 404–413.

Newcombe, R. (1998a), Two-sided confidence intervals for the single proportion: Comparison of seven methods, Statistics in Medicine,17, 857-872.

Rosner, B. (2010), Fundamentals of Biostatistics. Seventh Edition. Equation 5.15, page 133. Duxbury Press.

Vollset, S.E. (1993). Confidence intervals for a binomial proportion, Statistics in Medicine, 12, 809–824.