Basic Statistical Templates

Sample Size Discrete Example

Click SigmaXL > Templates & Calculators > Basic Statistical Templates > Sample Size Discrete to access the Sample Size Discrete calculator. The template gives the following default example:

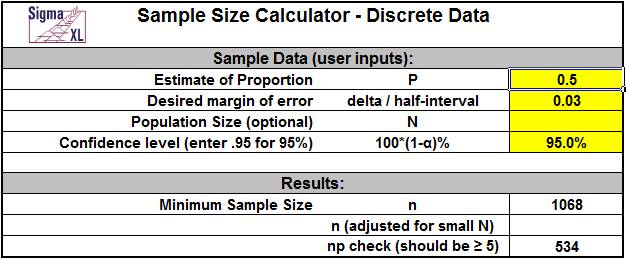
Notes for use of the Sample Size Discrete Calculator:

1. P is estimate of proportion for outcome of interest. Use P = 0.5 if unknown.
2. Delta is desired proportion margin of error. Enter as the half-width, i.e. if the desired margin of error is +/- 3%, enter 0.03.
3. Enter population size N to adjust for small populations (N < 10000).
4. np should be >= 5. If necessary, reduce delta to adjust.
5. Power (1 Beta) is not considered in these calculations. Power and Sample Size may be calculated using SigmaXL > Statistical Tools > Power & Sample Size Calculators.

This sample size calculator is based on a confidence interval approach, where you enter the desired half-interval value (delta). Lets say that you desire the proportion margin of error to be +/- 3%. As noted above, you simply enter a delta (half-interval) value of .03.

The challenge with this sample size calculator is that we need an estimate of the population proportion.This is a bit of a chicken and egg situation which comes first? I want to calculate an appropriate sample size to determine an outcome, but I am being asked to enter an estimate of the population proportion. First, keep in mind that this tool is a planning tool the true confidence intervals will be determined after you collect your data. Estimating the population proportion can be done if you have good historical data to draw from, for example, in historical customer surveys the percentage of satisfied customers was 80%. In this case you could use P=0.8. If you do not have a priori knowledge, then leave P=0.5 which gives the most conservative value (i.e., largest estimate of sample size).If you enter a value other than 0.5 it will result in a smaller sample size requirement.

Sample Size Continuous Example

Click SigmaXL > Templates & Calculators > Basic Statistical Templates > Sample Size Continuous to access the Sample Size Continuous calculator. The template gives the following default example:

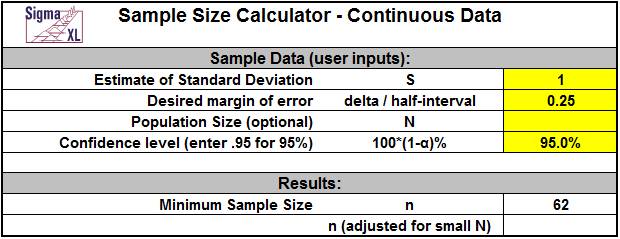
Notes for use of the Sample Size Continuous Calculator:

1. Delta uses the same units as the standard deviation. Enter as the half-width, i.e., if the desired margin of error is +/- 0.25, enter 0.25.
2. Enter (optional) population size N to adjust for small populations (N < 1000).
3. Power (1 Beta) is not considered in these calculations. Power and Sample Size may be calculated using SigmaXL > Statistical Tools > Power & Sample Size Calculators.

Similar to the Sample Size Discrete calculator, this sample size calculator is based on a confidence interval approach, where you enter the desired half-interval value (delta). If a survey had responses that were on a continuous scale of 1 to 5, and you desired a margin of error on the mean to be +/- .25, then you would use .25 as the delta value.Note that in this continuous case the units are not percentages but level of satisfaction.

Here we need an a priori estimate of the population standard deviation.If you have no idea what the standard deviation will be, then you could take a small sample to get a rough estimate of the standard deviation.