Spectral.html
- Home /
- Spectral.html

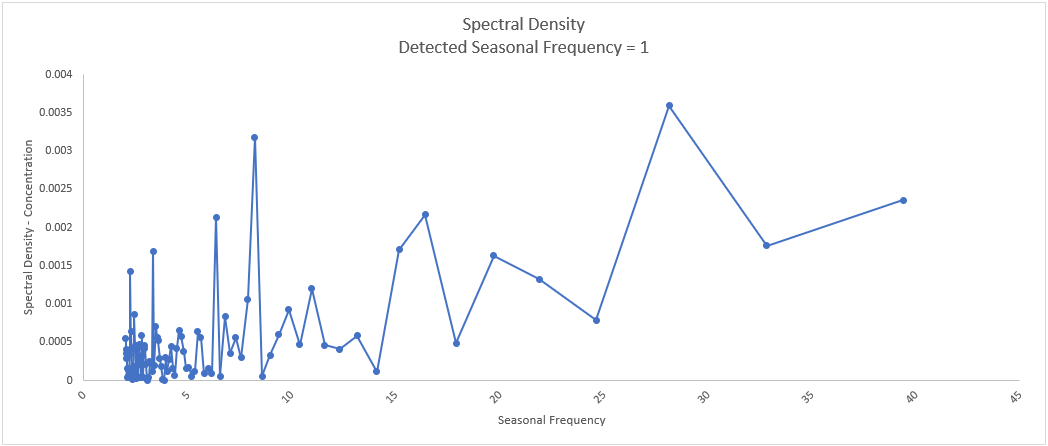 The detected seasonal frequency is 1, which means that it is a nonseasonal process. The
peak at 28 does not have enough seasonal strength to be considered for use as seasonal
frequency in a time series model.
The detected seasonal frequency is 1, which means that it is a nonseasonal process. The
peak at 28 does not have enough seasonal strength to be considered for use as seasonal
frequency in a time series model.
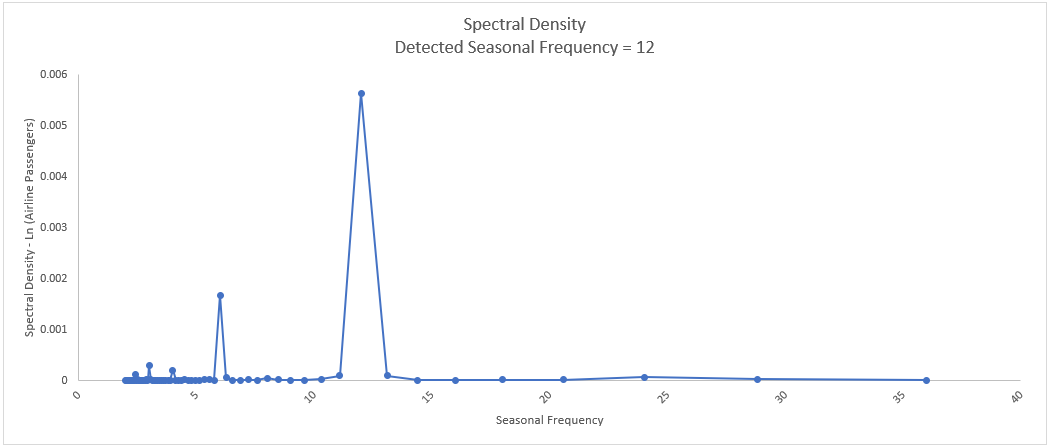 As expected, the detected seasonal frequency for the monthly data is 12. The peak at 6
does not have enough seasonal strength to be considered as a second seasonal
frequency.
As expected, the detected seasonal frequency for the monthly data is 12. The peak at 6
does not have enough seasonal strength to be considered as a second seasonal
frequency.
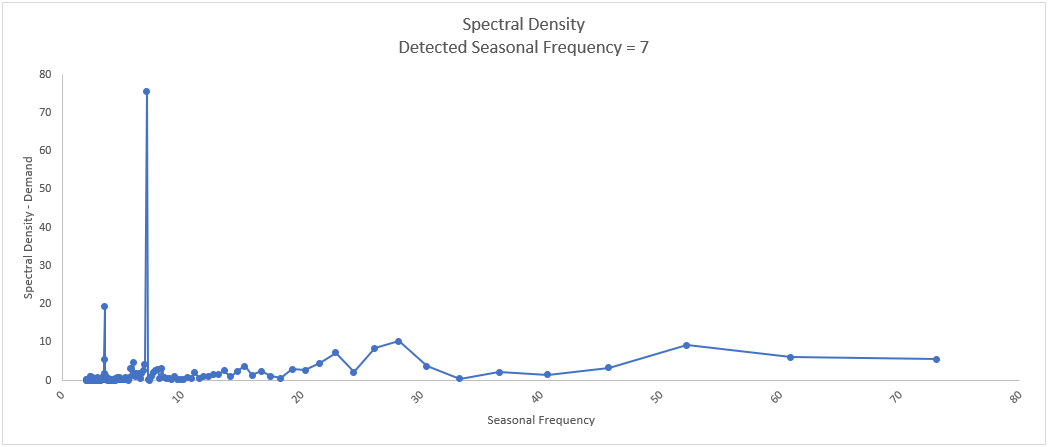 As expected, the detected seasonal frequency for the daily data is 7.
As expected, the detected seasonal frequency for the daily data is 7.
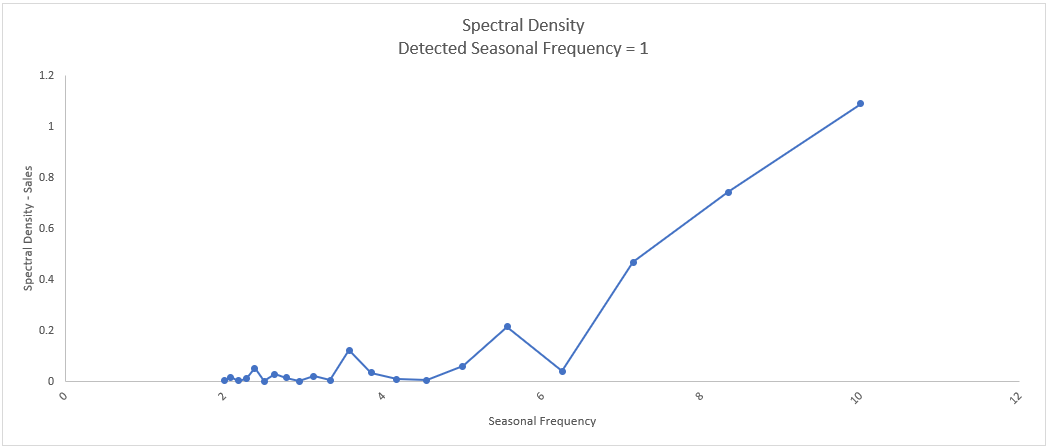 The detected seasonal frequency is 1, which means that it is confirmed to be a
nonseasonal process. The peak at 10 does not have enough seasonal strength to be
considered for use as
seasonal frequency in a time series model.
The detected seasonal frequency is 1, which means that it is confirmed to be a
nonseasonal process. The peak at 10 does not have enough seasonal strength to be
considered for use as
seasonal frequency in a time series model.
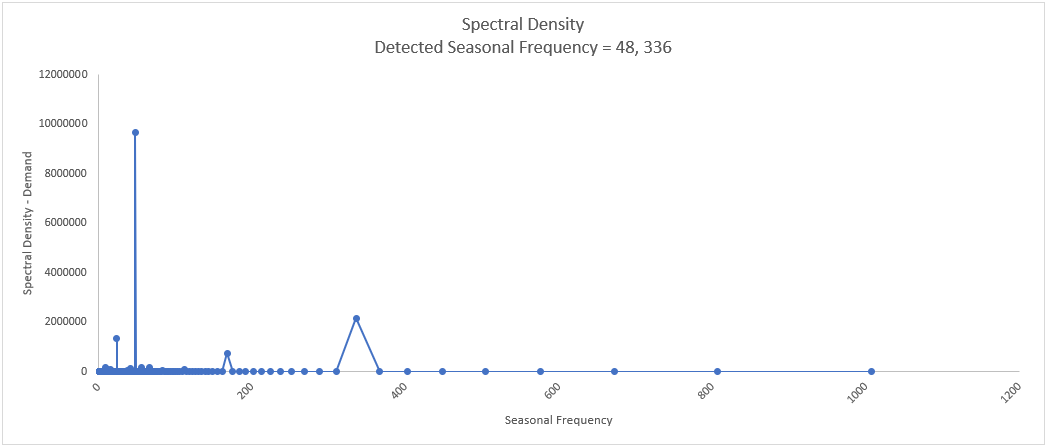 The detected multiple seasonal frequency is confirmed as 48, 336.
The detected multiple seasonal frequency is confirmed as 48, 336.