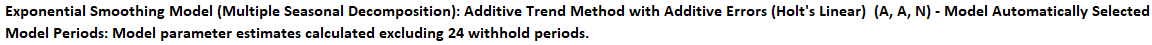Exponential Smoothing (MSD)

Exponential Smoothing Multiple Seasonal Decomposition (MSD) Forecast

Exponential Smoothing is limited to a maximum seasonal frequency of 24. For higher frequencies use Exponential Smoothing Multiple Seasonal Decomposition (MSD). The seasonal component is first removed through decomposition, a nonseasonal exponential smooth model fitted to the remainder (+trend), and then the seasonal component is added back in. For forecasting, a nave seasonal forecast is used on the seasonal component. Note that the prediction intervals are derived from the exponential smoothing model and do not include uncertainty in the seasonal component.

As the name implies, Multiple Seasonal Decomposition (MSD) also accommodates multiple seasonality, for example the half-hourly data with a seasonal frequency of 48 observations per day and 336 observations per week. When using MSD, it is recommended to limit the forecast period to 2*dominant seasonal frequency.

Monthly Airline Passengers - Series G

1. Open Monthly Airline Passengers - Series G.xlsx (Sheet 1 tab). This is the Series G data from Box and Jenkins, monthly total international airline passengers for January 1949 to December 1960. See the Run Chart, ACF/PACF Plots, Spectral.html and Seasonal Trend Decomposition Plots for this data. The Multiple Seasonal Decomposition (MSD) option is not necessary for this data, but by way of introduction, we will use this to compare to the previous analysis.
   
   
2. Click SigmaXL > Time Series Forecasting > Exponential Smoothing Forecast > Multiple Seasonal Decomposition Forecast. Ensure that the entire data table is selected. If not, check Use Entire Data Table. Click Next.
   
   
3. Select Monthly Airline Passengers, click Numeric Time Series Data (Y) >>. Select Date, click Optional Time Axis Labels >>. Check Display ACF/PACF/LB Plots and Display Residual Plots. Check Specify Model Periods. Set Withhold Periods = 24. Select Withhold Forecast Type: Multi-Step-Ahead with Prediction Interval at Start of Withhold. Select Seasonal Frequency Specify and enter 12. Check Box-Cox Transformation and select Rounded Lambda. We will use the default Prediction Interval = 95.0 %.

   
   
   Seasonal Frequency can have multiple entries however, we recommend no more than 3 values.
   
   

4. Click Model Options.
   
   
   
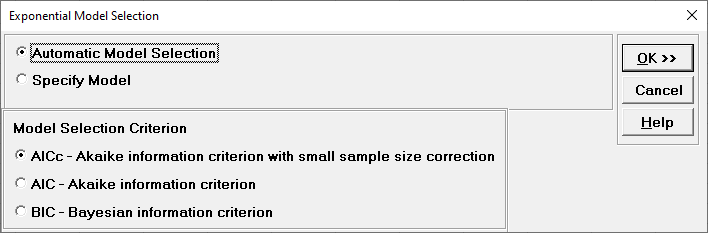
5. We will use the default Automatic Model Selection with AICc as the Model Selection Criterion. Click OK to return to the Exponential Smoothing MSD Forecast dialog. Click OK. The exponential smoothing forecast report is given:
   
   
   
   
6. Scroll down to view the Exponential Smoothing Model header:
   
   
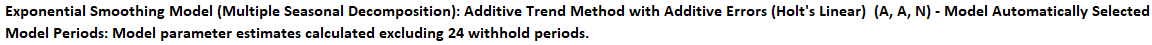
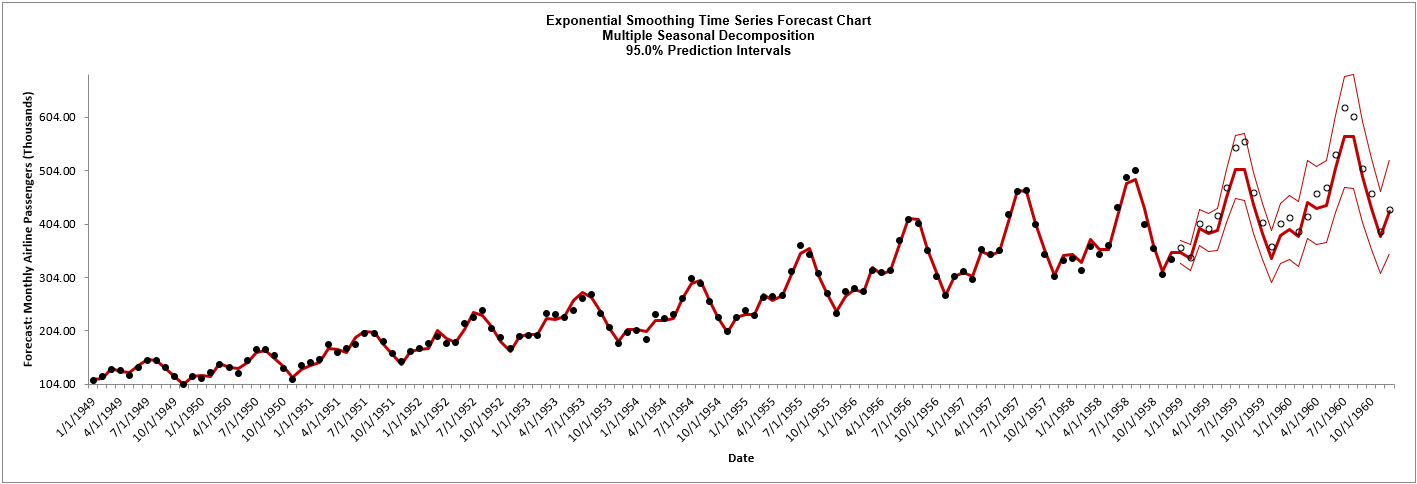
   After Multiple Seasonal Decomposition, the model is Additive Trend Method with Additive Errors (Holts Linear) (A, A, N).
   
   (A, A, N) was automatically selected as the best fit for the deseasonalized Airline Passenger data based on the AICc criterion.
   
   The header also includes the number of specified withhold periods.
   
   
7. The Exponential Smoothing Model Summary is given as:
   
   
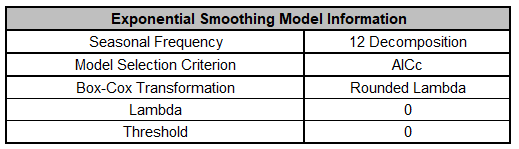
   This is a summary of the model information with Seasonal Frequency = 12 using Decomposition and Model Selection Criterion = AICc. The Box-Cox Transformation is Rounded Lambda with Lambda = 0 (Ln transformation).
   
   
8. The Parameter Estimates for the deseasonalized Airline Passenger data are:
   
   
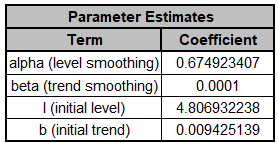
   Error includes the smoothing parameter alpha and initial level value (l). The error is additive, but on the Ln transformed data.
   
   Trend adds a smoothing parameter (beta) and initial trend value (b).
   
   Seasonal smoothing parameter (gamma) and initial seasonal values are not computed because the data has been deseasonalized.
   
   
9. The Exponential Smoothing Model Statistics are:
   
   
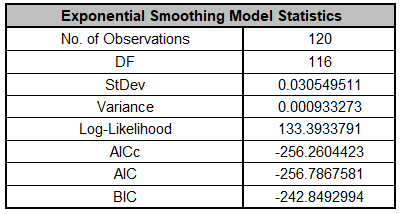
   The number of observations, n = 144 24 (withhold) = 120
   
   Degrees of freedom (DF) = 120 (n) 3 (2 terms in the model, 1 nonseasonal difference) = 117
   
   Note that the model statistics are based on the Ln transformed data, not the original data.
   
   The model statistics are better than the previous analysis: lower StDev and Variance, higher Log-Likelihood and lower AICc, AIC and BIC. This is to be expected because the data has been deseasonalized so the seasonal error component is not included.
   
   
10. The Forecast Accuracy metrics are:
    
    
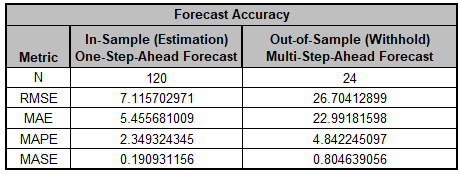
    Comparing to our earlier analysis, both the In-Sample (Estimation) One-Step-Ahead Forecast errors and Out-of Sample (Withhold) Multi-Step-Ahead Forecast errors are slightly smaller. (This was not expected, typically a Seasonal Exponential Smoothing or ARIMA model would give a more accurate forecast, based on comparison of methods using forecast competition data). However, given that we are forecasting out for two years, both models look very good..
    
    Forecast Accuracy metrics are calculated using the actual raw data versus inverse transformed forecast as displayed in the Forecast Chart and Table, so allow comparison across all model types and transformations.
    
    
11. Click on the Exp Smooth MSD ACF PACF LB sheet to view the ACF/PACF/LB Plots:
    
    
    
    
    
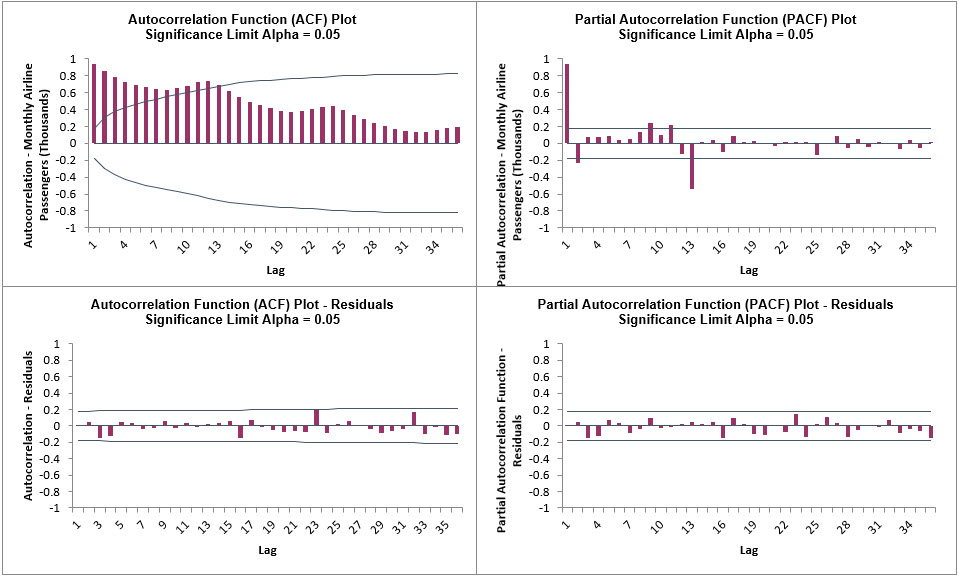
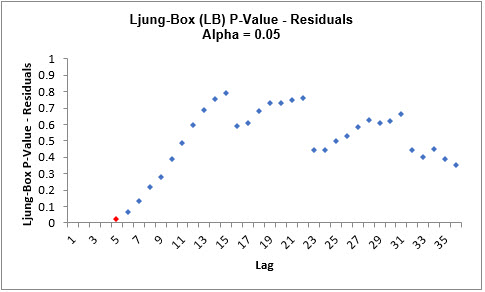
    The ACF/PACF Residuals Plots are similar to the previous analysis and indicate that almost all of the autocorrelation has been accounted for in the model, however the Ljung-Box plot confirms that this is a better fit, with most P-Values being blue (> .05).
    
    
12. Click on the Exp Smooth MSD Residuals sheet to view the Residual Plots:
    
    
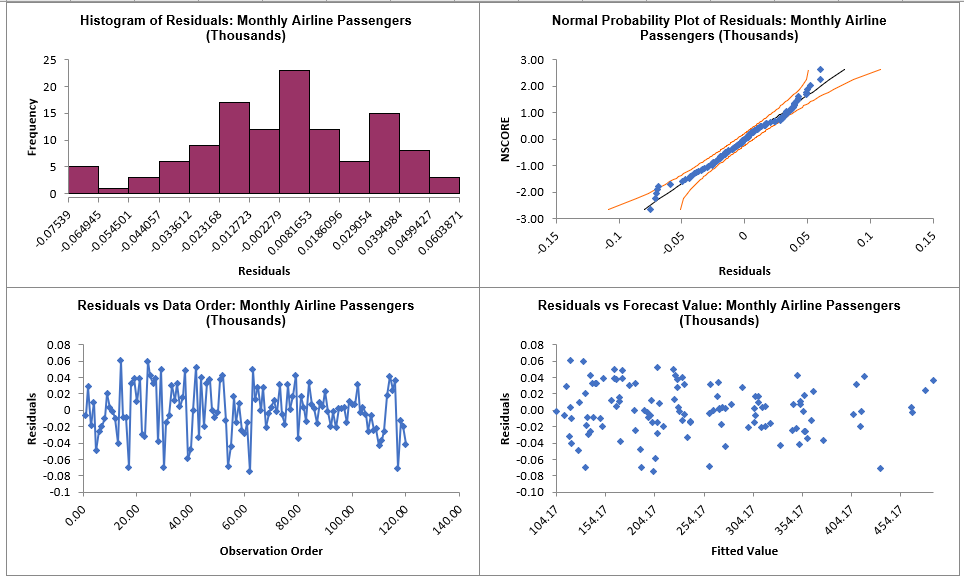
    The residuals are approximately normally distributed, with a roughly straight line on the normal probability plot. There are no obvious extreme outliers or patterns in the charts.
    
    Note that Residuals for MSD are the final observed -predicted values, so there are no scaling differences if the model uses additive or multiplicative error. Since a Box-Cox transformation was used, the residuals are in Ln transformed units.

Half-Hourly Multiple Seasonal Electricity Demand Taylor

13. Open Half-Hourly Multiple Seasonal Electricity Demand - Taylor.xlsx (Sheet 1 tab). This is half-hourly electricity demand (MW) in England and Wales from Monday, June 5, 2000 to Sunday, August 27, 2000 (taylor, R forecast). This data has multiple seasonality with frequency = 48 (observations per day) and 336 (observations per week), with a total of 4032 observations. See the Run Chart, ACF/PACF Plots, Spectral.html and Seasonal Trend Decomposition Plots for this data.


14. Click SigmaXL > Time Series Forecasting > Exponential Smoothing Forecast > Multiple Seasonal Decomposition Forecast. Ensure that the entire data table is selected. If not, check Use Entire Data Table. Click Next.


15. Select Demand, click Numeric Time Series Data (Y) >>. Check Display ACF/PACF/LB Plots and Display Residual Plots. Check Specify Model Periods. Set Withhold Periods = 96. Select Withhold Forecast Type: Multi-Step-Ahead with Prediction Interval at Start of Withhold. Check Seasonal Frequency with Specify = 48 336. Leave Box-Cox Transformation unchecked. We will use the default Prediction Interval = 95.0 %.



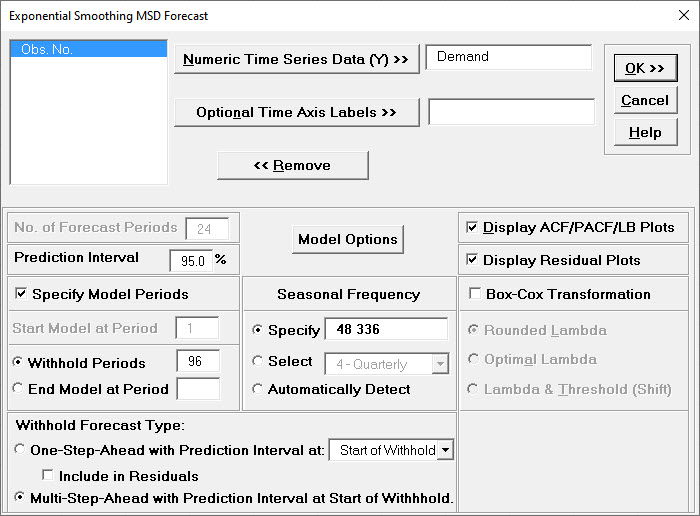
Withhold Periods is 2*dominant seasonal frequency (48). Dominant frequency is obtained from the Spectral.html. Start Model at Period = 1 is always greyed out for MSD.


16. Click Model Options.




17. We will use the default Automatic Model Selection with AICc as the Model Selection Criterion. Click OK to return to the Exponential Smoothing MSD Forecast dialog. Click OK. The exponential smoothing forecast report is given:




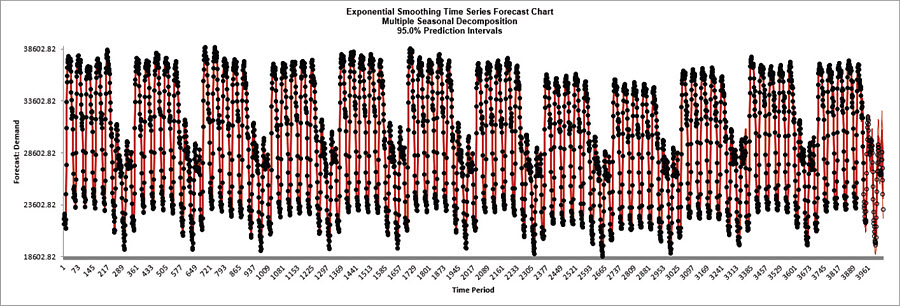
18. We will want to zoom in on the last 3 days, i.e., 144 half-hourly time periods, using chart scrolling. Click SigmaXL Chart Tools > Enable Scrolling .



You may be prompted with a warning message that custom formatting on the chart will be cleared. You can avoid seeing this warning by checking Save this choice as default and do not show this form again.


19. Click OK. The scroll dialog appears allowing you to specify the Start Period and Window Width. Enter Start Period = 3888 and Window Width = 144:



At any point, you can click Restore/Show All Data Points or Freeze Chart. Freezing the chart will remove the scroll and unload the dialog. The scroll dialog will also unload if you change worksheets. To restore the dialog, click SigmaXL Chart Tools > Enable Scrolling.


20. Click OK. A scroll bar appears beneath the forecast chart. You can also change the Start Subgroup and Window Width and Update.



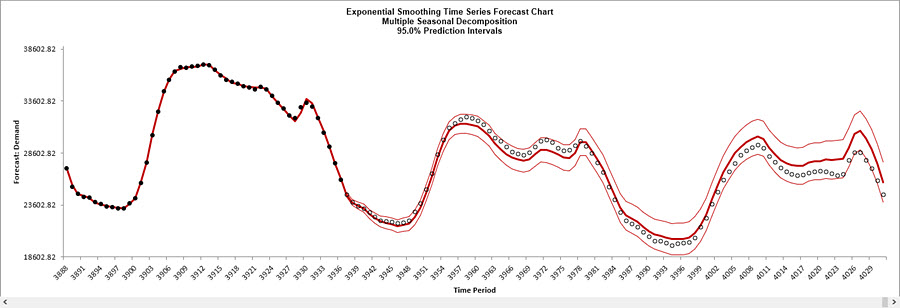
You can scroll through by clicking to the right or left, with the specified window width of 144.

The blank dots are the data values in the withhold sample with a multi-step forecast and prediction intervals displayed at the start of the withhold sample. The model does quite well at predicting the withhold 96 half-hour demand values. Note that the prediction error increases the further out we predict.

Click Cancel to exit the scroll dialog.


21. Scroll down to view the Exponential Smoothing Model header:



After Multiple Seasonal Decomposition, the model is Simple Exponential Smoothing with Multiplicative Errors (M, N, N).

(M, N, N) was automatically selected as the best fit for the deseasonalized Demand data based on the AICc criterion.

The header also includes the number of specified withhold periods.


22. The Exponential Smoothing Model Information is given as:



This is a summary of model information with Seasonal Frequency = 48, 336 using decomposition and Model Selection Criterion = AICc.


23. The Parameter Estimates for the deseasonalized Demand data are:




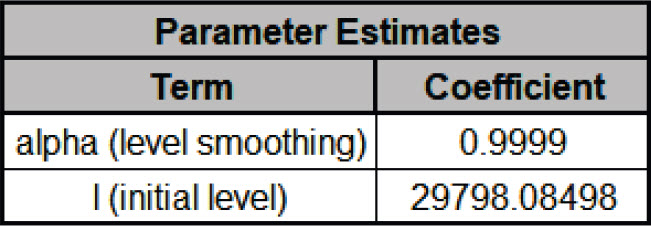
• Error includes the smoothing parameter alpha and initial level value (l). With alpha = 0.9999, this is effectively a nave forecast, with multiplicative errors.


• Seasonal smoothing parameter (gamma) is not computed because the data has been deseasonalized.


24. The Exponential Smoothing Model Statistics are:




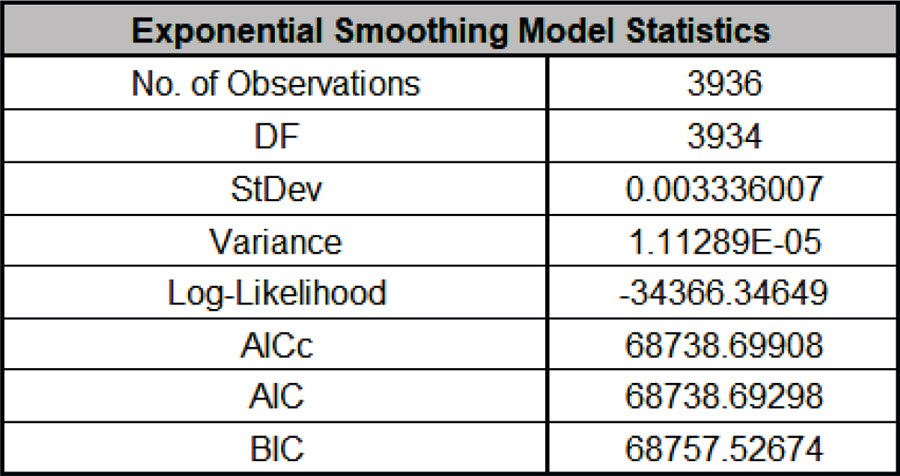
• The number of observations, n = 4032 96 (withhold) = 3936


• Degrees of freedom (DF) = 3936 (n) 2 (terms in the model) = 3934


• Note that the model statistics are calculated using the deseasonalized data and residuals are multiplicative (relative) errors:

  et =	yt - ŷt
  	ŷt

   
25. The Forecast Accuracy metrics are:



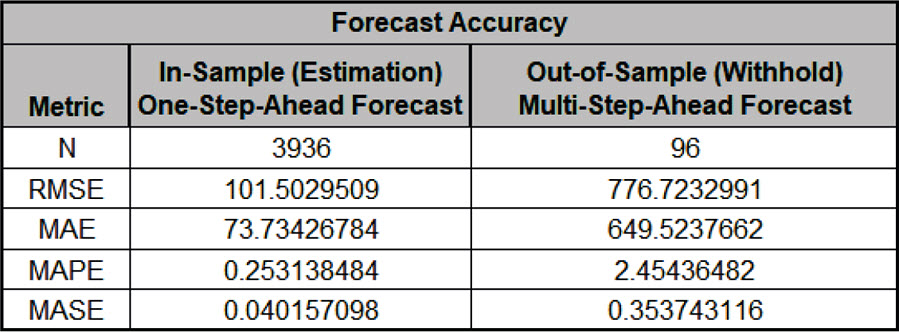
As expected, the Out-of Sample (Withhold) Multi-Step-Ahead Forecast errors are larger than the In-Sample (Estimation) One-Step-Ahead Forecast errors. Note, if we were primarily interested in a short term one-step ahead forecast, then we would have selected Withhold Forecast Type: One-Step-Ahead and the above table would show Out-of Sample (Withhold) One-Step-Ahead Forecast errors.

Forecast Accuracy metrics are calculated using the actual raw data versus forecast as displayed in the Forecast Chart and Table so, unlike the model statistics above, allows comparison across all forecast model types and transformations.


26. The Forecast Table is given as:



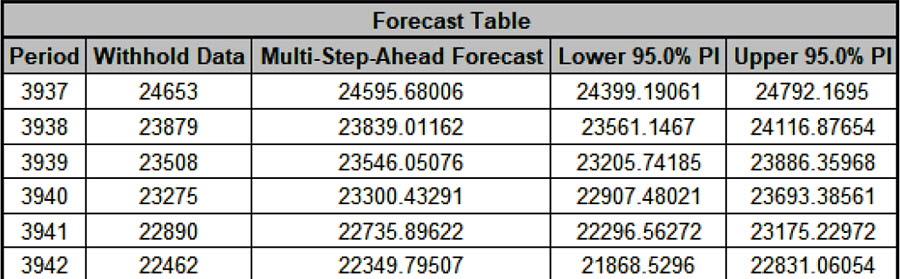
These are the same forecast and prediction interval values displayed in the Forecast Chart, but provided for further analysis or charting (e.g., a run chart of the forecast errors). The Withhold Data is also displayed.


27. Click on the Exp Smooth MSD ACF PACF LB sheet to view the ACF/PACF/LB Plots:





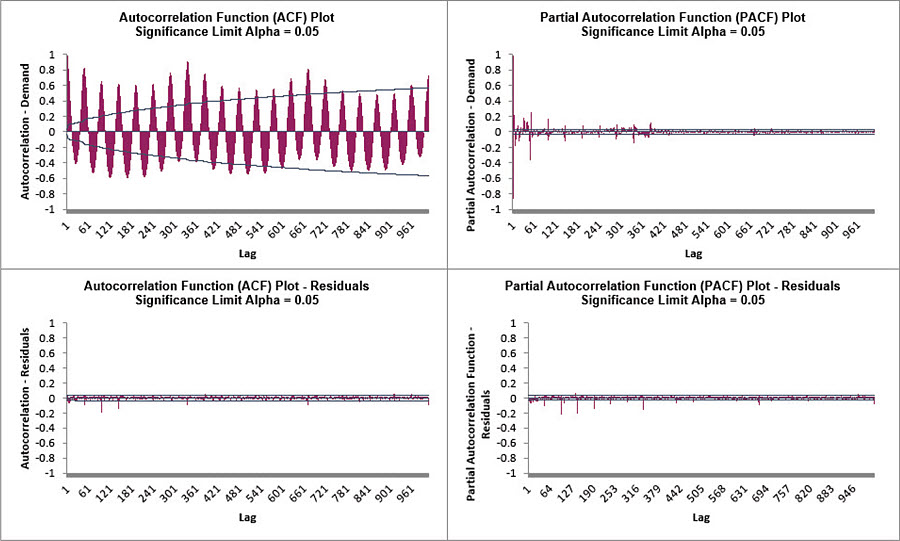
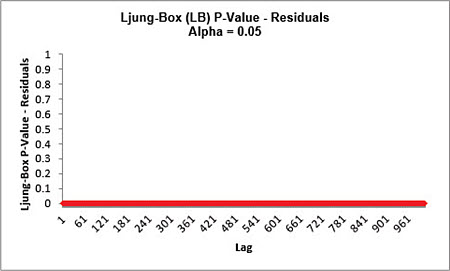
The ACF/PACF Residuals Plots indicate that much of the autocorrelation has been accounted for in the model, but the Ljung-Box plot shows that some significant autocorrelation still remains (the red P-Values are significant at alpha=.05) - so the model can potentially be improved. This does not mean that the model is a bad model, it can still be very useful for prediction purposes, but the prediction intervals may not provide accurate coverage.


28. Click on the Exp Smooth MSD Residuals sheet to view the Residual Plots:



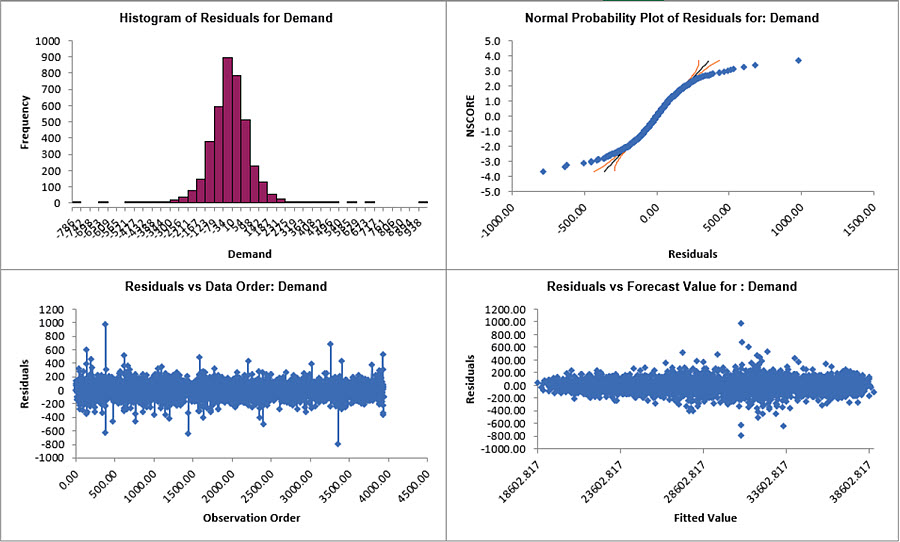
The residuals are not normally distributed and there are extreme outliers. These should be investigated with a control chart on the residuals. Outliers in Electricity Demand are often explained by Temperature and this is something we will look at later with a different data set (Daily Electricity Demand with Predictors ElecDaily).


29. Note that Residuals for MSD are the final observed - predicted values, so there are no scaling differences if the model uses additive or multiplicative error. If a Box-Cox transformation is used, then the residuals are in transformed units.