Control Chart Templates: Time-Weighted

Average Run Length (ARL) Tables

Click SigmaXL > Templates & Calculators > Control Chart Templates > Time Weighted > Average Run Length (ARL) Tables.

This template is also located at SigmaXL > Control Charts > Control Chart Templates >
Time Weighted > Average Run Length (ARL) Tables.

Average Run Length (ARL) characteristics are very useful to compare the performance of control charts and determine optimal parameter settings for EWMA and CUSUM time weighted control charts. The ARL value for a shift in mean = 0 sigma is the “in-control” run length and is denoted as ARL0. ARL0 is 1/α, where α is the type I false alarm probability, so this should be as large as possible minimizing the likelihood that an out-of-control signal is a false alarm. In a Shewhart Individuals Control Chart, ARL0 = 1/α = 1/(0.00135*2) = 370.4. On average, we will see a false alarm once every 370 observations. Note that this is a mean of a geometric distribution, so in practice the actual ARL0 will vary widely with the standard deviation approximately equal to the mean value (See Montgomery [7]).

When we have a sustained shift in mean > 0, the ARL value is the “out-of-control” run length and is denoted as ARL1. ARL1 = 1/(1-β), where β is the type II miss probability and (1-β) is the power to detect. This should be as small as possible so that a shift in process mean is quickly detected.

When using EWMA or CUSUM charts, we typically set the parameters to minimize the ARL1 to give rapid detection for a small shift in mean of 1 sigma. Shewhart charts are typically used when trying to rapidly detect a large shift in mean of >= 3 sigma. Tests for special causes may be used with Shewhart to improve the small shift performance, but they give poor ARL0 performance resulting in frequent false alarms.

Subgroups improve the small shift performance of a Shewhart chart without impacting the ARL0 rate and if possible, should be used. In these tables, we are only considering Individuals, but this can be adjusted using the sigma of averages, sigma/√n. For example, with a subgroup size of 4, the ARL1 values in the tables at Shift in Mean = 2 give the ARL performance for a shift in mean = 1 sigma. A Shewhart Individuals chart (without additional tests for special causes) has an ARL1 (Shift in Mean = 1 sigma) of 44, a Shewhart X-bar chart with n=4 has an ARL1 value of 6.3.

ARL1
ARL2

Notes:

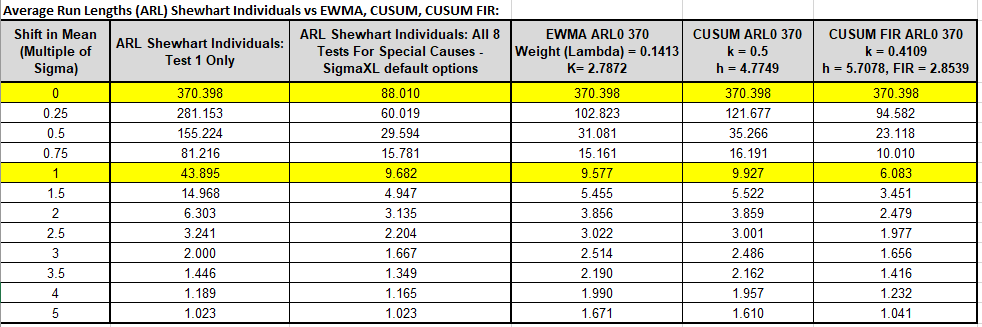
1. Assumes parameters are known and shift occurs at the start (zero state). Practically, this will not likely be the case in use, but it allows ARL comparison across chart types with recommended parameter settings.
2. ARL Shewhart Individuals: Test 1 Only uses Excel formula: =1/((1-NORM.S.DIST(3-A3,1))+(1-NORM.S.DIST(A3+3,1))).
3. ARL Shewhart Individuals All 8 Tests For Special Causes - SigmaXL default options calculated using Monte Carlo simulation with 1e6 replications.
4. EWMA ARL0 370, CUSUM ARL0 370 and CUSUM FIR ARL0 370 parameter values are optimized to minimize ARL for Shift in Mean = 1 Sigma while maintaining an ARL0 value = 370.4. See respective sheets for other optimal Shift in Mean values.
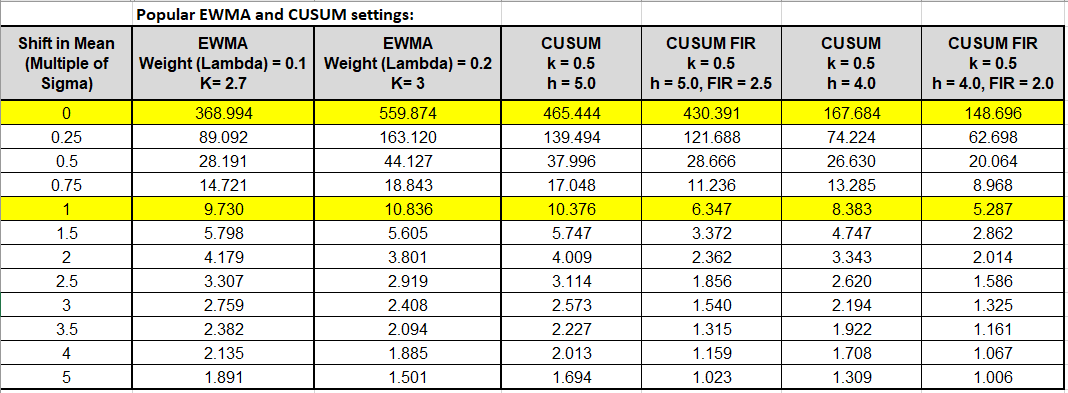
5. Comparison of ARLs for EWMA, CUSUM, CUSUM FIR with ARL0 500, 465 and 168 are given in separate sheets.
6. ARL for EWMA is calculated using xewma.arl in the R spc package (Knoth). Arguments: sided = "two"; limits = "fix". This function numerically solves the related ARL integral equation by means of the Nystroem method based on Gauss-Legendre quadrature.
7. ARL for CUSUM is calculated using xcusum.arl in the R spc package. Arguments: sided = "two".
8. EWMA K is calculated using xewma.crit function in the R spc package. R optimize is used with xewma.arl and xewma.crit to obtain optimal Weight (Lambda) values. See Bloomfield, Exponentially Weighted Moving Average Chart.
9. CUSUM h is calculated using xcusum.crit function in the R spc package. CUSUM FIR with 50% headstart uses R optimize with xcusum.arl and xcusum.crit to obtain optimal k and h values (excluding h = 5 and 4 example above). See Bloomfield, Cumulative Sum Control Chart.

REFERENCES:
[1] Bloomfield, P., “Statistical Methods for Quality and Productivity Improvement / Statistical Process Control”, ST435/535 course slides, Exponentially Weighted Moving Average Chart, https://www.stat.ncsu.edu/people/bloomfield/courses/st435-535/slides/Montgomery-ch09-sec02-03.pdf
[2] Bloomfield, P., “Statistical Methods for Quality and Productivity Improvement / Statistical Process Control”, ST435/535 course slides, Cumulative Sum Control Chart, https://www.stat.ncsu.edu/people/bloomfield/courses/ST435-535/slides/Montgomery-ch09-sec01-01.pdf
[3] Crowder, S.V. (1989), “Design of Exponentially Weighted Moving Average Schemes”, Journal of Quality Technology, 21:3, 155-162, Tables 4, 6.
[4] Knoth, S. (2019), “spc: Statistical Process Control – Calculation of ARL and Other Control Chart Performance Measures”, R package, version 0.6.3: https://cran.r-project.org/web/packages/spc/index.html
[5] Lucas, J.M. and Crosier R.B. (1982), “Fast initial response for cusum quality-control schemes: Give your cusum a headstart”, Technometrics 24, 199-205, Table 1.
[6] Lucas J.M. and Saccucci M.S. (1990), “Exponentially weighted moving average control schemes: Properties and enhancements”, Technometrics 32, 1-12, Figures 3, 4.
[7] Montgomery, D.C. (2013), Introduction to Statistical Quality Control, Seventh Ed., Wiley, pp. 199-201 and Tables 9.5, 9.11.