How Do I Perform a Reliability/Weibull Analysis in Excel Using SigmaXL?
Reliability/Weibull Analysis
The Weibull distribution is a continuous distribution that was publicized by Waloddi Weibull in 1951. It has become widely used, especially in the reliability field. The Weibull distribution's popularity resulted from its ability to be used with small sample sizes and its flexibility. See Dodson, B. “The Weibull Analysis Handbook” Second Edition, ASQ, for further information.The Weibull distribution can also be used as an alternative to the Box-Cox Transformation to determine Process Capability Indices or Control Limits for non-normal data.
Weibull is particularly effective when the data are censored, with exact failure times unknown or suspension of test. Suspension of test is also referred to as right censored. SigmaXL can analyze complete or right censored data.
- Open the file Weibull Dodson.xlsx. This contains right censored time-to-failure data from Dodson, page 28.
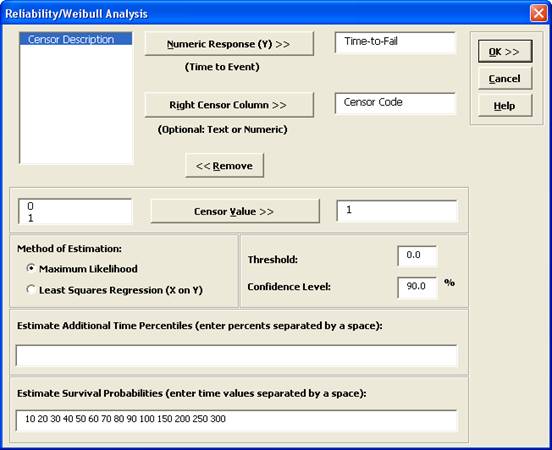
- Click SigmaXL > Reliability/Weibull Analysis. Ensure that the entire data table is selected. Click Next.
- Select Time-to-Fail, click Numeric Response (Y) >>. Note that the selected variable must contain all positive values. Select Censor Code, click Right Censor Column >>. The default censor value of 1 will be used. We will use the default method of estimation, Maximum Likelihood (some reliability practitioners prefer Least Squares Regression (X on Y) for small sample sizes). Other defaults include Threshold = 0, and Confidence Level = 90%. Enter time values to estimate survival probabilities as shown:
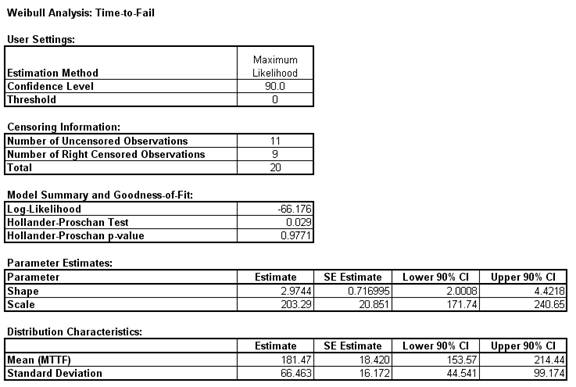
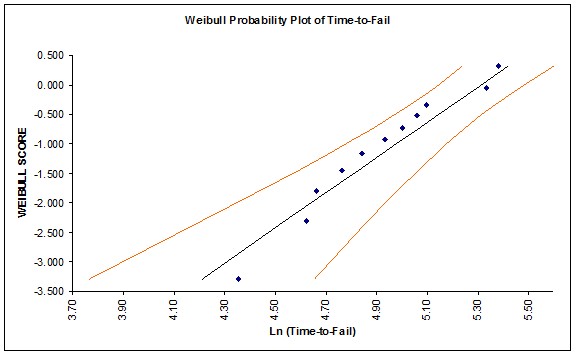
- The resulting Weibull analysis report is shown:
- The Hollander-Proschan test is used when there are right censored observations (see Dodson). If the p-value is less than 0.05, this indicates significant lack of fit, so Weibull would not be an appropriate distribution. Given the p-value of 0.9771, there is no lack-of-fit with this time-to-fail data. This is confirmed in the Weibull probability plot with the data roughly following a straight line.
- If the data is uncensored then the Anderson-Darling unadjusted test is used.
- The shape parameter, also referred to as Beta, is the slope of the line on the Weibull probability plot. The Weibull distribution can be used in a wide variety of situations and dependent on the value of Beta, is equal to or can approximate several other distributions. For example, if Beta = 1, the Weibull distribution is identical to the exponential distribution; if Beta = 2.5, the Weibull distribution approximates the lognormal distribution; and if Beta = 3.6, the Weibull distribution approximates the normal distribution. Because of this flexibility, there are few observed failure rates that cannot be accurately modeled by the Weibull distribution. Furthermore if Beta is < 1, the system is suffering from infant mortality failures; if Beta is = 1, failures are random – they are occurring at a constant failure rate and are independent of time; if Beta is > 1, components are wearing out with age.
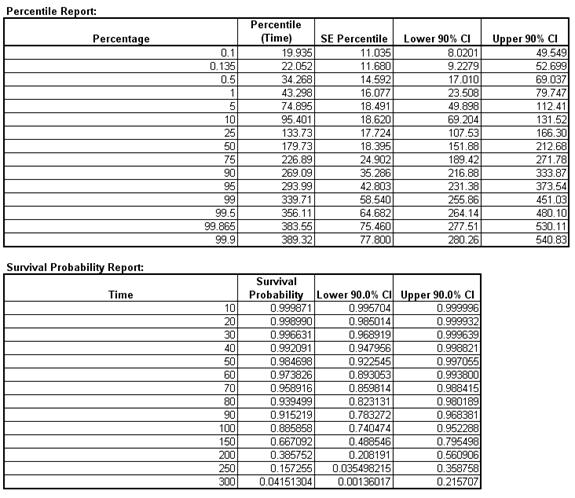
- The scale parameter is the characteristic life. This is the point at which we could expect 63.2% of the population under study to have failed. The survival probability report shows that the survival probability at time 200 = 0.386. The cumulative failure probability at 200 is 1 – 0.386 = 0.614.
- The percentile report tells us that we can expect a 50% failure rate (one-half of the population will fail) at time = 179.73, i.e. the Median = 179.73.
- The percentile report can also be used to determine control limits for non-normal data. The lower control limit is the 0.135 % value = 22.052; the center line is the 50% value = 179.73; the upper control limit is the 99.865 % value = 383.55.
Web Demos
Our CTO and Co-Founder, John Noguera, regularly hosts free Web Demos featuring SigmaXL and DiscoverSim
Click here to view some now!
Contact Us
Phone: 1.888.SigmaXL (744.6295)
Support: Support@SigmaXL.com
Sales: Sales@SigmaXL.com
Information: Information@SigmaXL.com