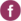How Do I Create an Attribute MSA Report in Excel Using SigmaXL?
Attribute MSA (Binary)
Attribute MSA is also known as Attribute Agreement Analysis. Use
the Binary option if the assessed result is text or numeric binary
(e.g., 0/1, Pass/Fail, Good/Bad, G/NG, Yes/No).
- Open the file Attribute MSA – AIAG.xlsx. This is an example from the Automotive Industry Action Group (AIAG) MSA Reference Manual, 3rd edition, page 127 (4th Edition, page 134). There are 50 samples, 3 appraisers and 3 trials with a 0/1 response. A “good” sample is denoted as a 1. A “bad” sample is denoted as a 0. Note that the worksheet data must be in stacked column format and the known reference values must be consistent for each sample.
- Click SigmaXL > Measurement Systems Analysis > Attribute MSA (Binary). Ensure that the entire data table is selected. Click Next.
- Select Part, Appraiser, Assessed
Result and Reference as shown. Check
Report Information and enter AIAG Attribute
MSA Binary for Product/Unit Name. Select
Percent Confidence Interval Type – Exact. The
default Good Level of “1”will be used as
specified in the AIAG manual:
Tip: The Good Level definition is used to determine Type I and Type II error rates. It is applicable only when a True Standard is selected.
Tip: Percent Confidence Interval
Type applies to the Percent Agreement and Percent Effectiveness
Confidence Intervals. These are binomial proportions that have an
"oscillation" phenomenon where the coverage probability varies with
the sample size and proportion value. Exact is
strictly conservative and will guarantee the specified confidence
level as a minimum coverage probability, but results in wider
intervals. Wilson Score has a mean coverage
probability that matches the specified confidence interval. Since
the intervals are narrower and thereby more powerful, Wilson Score
is recommended for use in attribute MSA studies due to the small
sample sizes typically used. Exact is selected in
this example for continuity with the results from SigmaXL Version 6.
- Click OK. The Attribute MSA Binary
Analysis Report is produced. The tables and associated graphs are described
separately by section for clarity.
Tip: While this report is quite extensive, a quick assessment of
the attribute measurement system can be made by viewing the Kappa
color highlights: Green - very good agreement (Kappa >= 0.9); Yellow
- marginally acceptable, improvement should be considered (Kappa 0.7
to < 0.9); Red - unacceptable (Kappa < 0.7). Further details on
Kappa are given below.
Within Appraiser Agreement
is an assessment of each appraiser’s consistency of ratings across
trials and requires at least two trials. This is analogous to Gage
R&R Repeatability. Note that the reference standard is not
considered, so an appraiser may be perfectly consistent but
consistently wrong!
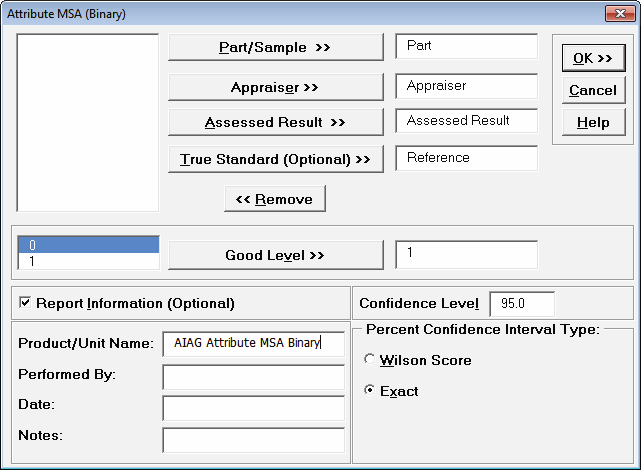
Percent/CI: Within Appraiser
Agreement Graph:
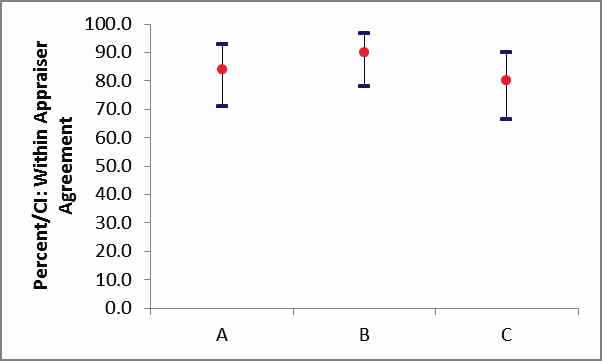
Kappa/CI: Within Appraiser Agreement
Graph:
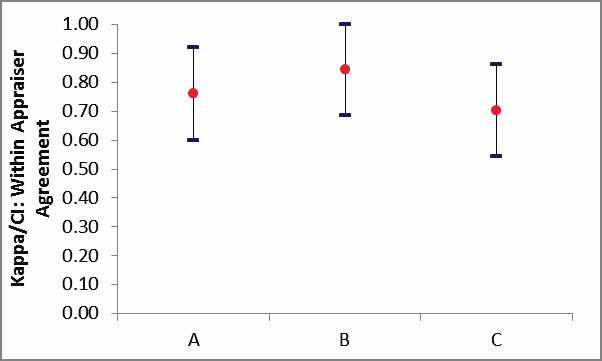
Within Appraiser Agreement Table:

Tip: The Percent/CI
Within Appraiser Agreement Graph can be used to compare
relative consistency of the appraisers, but should not be used as an
absolute measure of agreement. Within Appraiser Percent
Agreement will decrease as the number of trials increase
because a match occurs only if an appraiser is consistent across all
trials. Use the Kappa/CI: Within Appraiser Agreement
Graph to determine adequacy of the Within Appraiser agreement. See
below for additional interpretation guidelines.
Tip: Hover the mouse
pointer over the heading cells to view the following report
comments.
# Inspected: Number of
parts or samples.
# Matched: A match occurs
only if an appraiser is consistent across all trials.
Percent Agreement =
(# Matched / # Inspected) * 100
LC = Percent Lower
Confidence Limit. UC = Percent Upper Confidence
Limit. Confidence intervals (CI) for binomial proportions have an
"oscillation" phenomenon where the coverage probability varies with
n and p. Exact is strictly conservative and will
guarantee the specified confidence level as a minimum coverage
probability, but results in wide intervals. Wilson Score has a mean
coverage probability that matches the specified confidence interval.
Since the intervals are narrower and thereby more powerful, they are
recommended for use in attribute MSA studies due to the small sample
sizes typically used. See Appendix
Percent Confidence Intervals (Exact Versus Wilson Score)
for references.
Fleiss’ Kappa statistic is
a measure of agreement that is analogous to a “correlation
coefficient” for discrete data. Kappa ranges from -1 to +1: A Kappa
value of +1 indicates perfect agreement. If Kappa = 0, then
agreement is the same as would be expected by chance. If Kappa = -1,
then there is perfect disagreement. “Rule-of-thumb”
interpretation guidelines: >= 0.9 very good agreement (green); 0.7
to < 0.9 marginally acceptable, improvement should be considered
(yellow); < 0.7 unacceptable (red). See Appendix Kappa for
further details on the Kappa calculations and “rule-of-thumb”
interpretation guidelines.
Fleiss’ Kappa P-Value: H0:
Kappa = 0. If P-Value < alpha (.05 for specified 95% confidence
level), reject H0 and conclude that agreement is not the same as
would be expected by chance. Significant P-Values are highlighted in
red.
Fleiss' Kappa LC (Lower
Confidence) and Fleiss' Kappa UC (Upper Confidence)
limits use a kappa normal approximation. Interpretation Guidelines:
Kappa lower confidence limit >= 0.9: very good agreement. Kappa
upper confidence limit < 0.7: the attribute agreement is
unacceptable. Wide confidence intervals indicate that the sample
size is inadequate.
In this example, we have marginal
Within Appraiser Agreement for each of the appraisers.
Each Appraiser vs. Standard
Agreement is an assessment of each appraiser’s ratings
across trials compared to a known reference standard. This is
analogous to Gage R&R Accuracy.
Percent/CI: Each Appraiser vs.
Standard Agreement Graph:
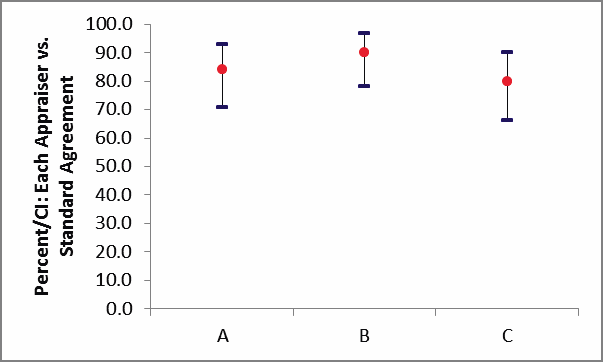
Each Appraiser vs. Standard
Agreement Table:

Tip: The Percent/CI
Each Appraiser vs. Standard Agreement Graph can be used to
compare agreement to standard across the appraisers, but should not
be used as an absolute measure of agreement. Each Appraiser
vs. Standard Agreement will decrease as the number of
trials increase because a match occurs only if an appraiser agrees
with the standard consistently across all trials. Use
Fleiss’ Kappa in the Each Appraiser vs. Standard
Agreement Table to determine the adequacy of Each Appraiser
versus Standard agreement.
# Inspected: Number of parts or samples.
# Matched: A match occurs only if an appraiser agrees with the
standard consistently across all trials.
Percent Agreement = (# Matched / # Inspected) * 100
Kappa is interpreted as above: >= 0.9 very good agreement
(green); 0.7 to < 0.9 marginally acceptable, improvement should be
considered (yellow); < 0.7 unacceptable (red).
Appraisers A and C have marginal agreement versus the standard
values. Appraiser B has very good agreement to the standard.
Each Appraiser vs. Standard Disagreement is a breakdown of each
appraiser’s rating misclassifications (compared to a known reference
standard). This table is applicable only to binary two-level
responses (e.g., 0/1, G/NG, Pass/Fail, True/False, Yes/No).

A Type I Error occurs when the appraiser consistently assesses a
good part/sample as bad. "Good" is defined by the user in the
Attribute MSA analysis dialog.
Type I Error % = (Type I Error / # Good Parts or Samples) * 100
A Type II Error occurs when a bad part/sample is consistently
assessed as good.
Type II Error % = (Type II Error / # Bad Parts or Samples) * 100
A Mixed Error occurs when the assessments across trials are not
identical.
Mixed Error % = (Mixed Error / # Parts or Samples) * 100
Between Appraiser Agreement is an assessment of the appraisers’
consistency of ratings across trials and between each other. At
least two appraisers are required. This is analogous to Gage R&R
Reproducibility. Note that the reference standard is not considered,
so the appraisers may be perfectly consistent, but consistently
wrong!
![]()
All Appraisers vs. Standard Agreement is an assessment of all
appraisers’ ratings across trials compared to a known reference
standard. This is analogous to Gage R&R Accuracy.
![]()
Kappa is interpreted as above:
>= 0.9 very good agreement
(green); 0.7 to < 0.9 marginally acceptable (yellow); < 0.7
unacceptable (red).
Since the Between Appraiser Agreement and All Appraisers vs.
Standard Agreement are marginally acceptable, improvements to the
attribute measurement should be considered. Look for unclear or
confusing operational definitions, inadequate training, operator
distractions or poor lighting. Consider the use of pictures to
clearly define a defect.
The Attribute Effectiveness Report is similar to the
Attribute
Agreement Report, but treats each trial as an opportunity.
Consistency across trials or appraisers is not considered. This has
the benefit of providing a Percent measure that is unaffected by the
number of trials or appraisers. Also, the increased sample size for
# Inspected results in a reduction of the width of the Percent
confidence interval. The Misclassification report shows all errors
classified as Type I or Type II. Mixed errors are not relevant here.
This report requires a known reference standard and includes:
Each
Appraiser vs. Standard Effectiveness, All Appraisers vs. Standard
Effectiveness, and Effectiveness and Misclassification Summary.
Each Appraiser vs. Standard Effectiveness is an assessment of
each appraiser’s ratings compared to a known reference standard.
This is analogous to Gage R&R Accuracy. Unlike the Each Appraiser
vs. Standard Agreement table above, consistency across trials is not
considered here - each trial is considered as an opportunity. This
has the benefit of providing a Percent measure that is unaffected by
the number of trials. Also, the increased sample size for #
Inspected results in a reduction of the width of the Percent
confidence interval.
Percent/CI: Each Appraiser vs. Standard Effectiveness Graph:
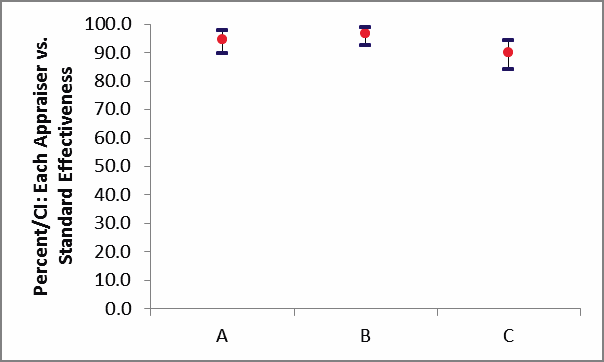
Kappa/CI: Each Appraiser vs. Standard
Effectiveness Graph:
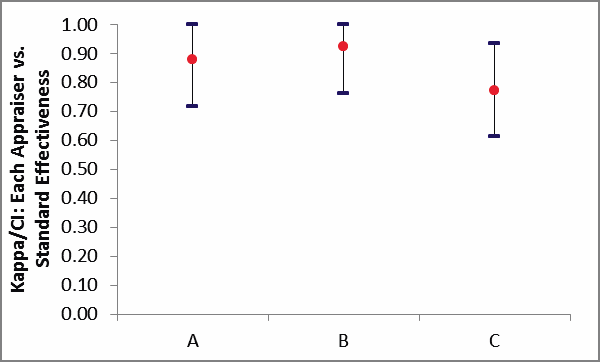
Each Appraiser vs. Standard Effectiveness
Table:

# Inspected = # Parts or Samples * # Trials
# Matched: A match occurs if an appraiser agrees with the
standard (consistency across trials is not considered here).
Percent Effectiveness = (# Matched / # Inspected) * 100.
Interpretation Guidelines for Percent Effectiveness: => 95% very
good; 85% to <95% marginal, may be acceptable but improvement should
be considered; < 85% unacceptable. These guidelines assume an equal
number of known good and known bad parts/samples.
Kappa is interpreted as above:
>= 0.9 very good agreement
(green); 0.7 to < 0.9 marginally acceptable (yellow); < 0.7
unacceptable (red).
Tip: The Kappa values in the Effectiveness tables are very
similar to those in the Agreement tables (the slight difference is
due to average Kappa for unstacked versus Kappa for stacked data).
This is why the Kappa/CI Each Appraiser vs. Standard Agreement graph
is not shown. It would essentially be a duplicate of the Kappa/CI
Each Appraiser vs. Standard Effectiveness graph.
Appraisers A and C have marginal agreement versus the standard
values, with less than 95% Effectiveness and Kappa < 0.9. Appraiser
B has very good agreement to the standard.
All Appraisers vs. Standard Effectiveness is an assessment of all
appraisers’ ratings compared to a known reference standard. This is
analogous to Gage R&R Accuracy. Unlike the All Appraiser vs.
Standard Agreement table above, consistency across trials and
appraisers is not considered here - each trial is considered as an
opportunity. This has the benefit of providing a Percent measure
that is unaffected by the number of trials or appraisers. Also, the
increased sample size for # Inspected results in a reduction of the
width of the Percent confidence interval.
![]()
# Inspected = # Parts or Samples * # Trials * # Appraisers
# Matched: A match occurs if an appraiser agrees with the
standard (consistency across trials and appraisers is not considered
here).
Percent Effectiveness =
(# Matched / # Inspected) * 100.
The interpretation guidelines for Kappa and Percent Effectiveness
are the same as noted above. This measurement system is marginally
acceptable.
Each Appraiser vs. Standard Misclassification is a breakdown of
each appraiser’s rating misclassifications (compared to a known
reference standard). This table is applicable only to binary
two-level responses (e.g., 0/1, G/NG, Pass/Fail, True/False,
Yes/No). Unlike the Each Appraiser vs. Standard Disagreement table
above, consistency across trials is not considered here. All errors
are classified as Type I or Type II. Mixed errors are not relevant.
![]()
A Type I error occurs when the appraiser assesses a good
part/sample as bad (consistency across trials is not considered
here). "Good" is defined by the user in the Attribute MSA analysis
dialog. See Misclassification Legend for specific definition of
Type
I and Type II Errors.
# Inspected = # Good Parts or Samples * # Trials
Type I Error % = (Type I Error / # Inspected Good) * 100
A Type II error occurs when a bad part/sample is assessed as
good. See Misclassification Legend for specific definition of
Type I
and Type II Errors.
# Inspected = # Bad Parts or Samples * # Trials * # Appraisers
Type II Error % = (Type II Error / # Inspected Bad) * 100
All Appraisers vs. Standard
Misclassification is a breakdown of all appraisers’ rating
misclassifications (compared to a known reference standard). This
table is applicable only to binary two-level responses (e.g., 0/1,
G/NG, Pass/Fail, True/False, Yes/No). Unlike the All
Appraisers vs. Standard Disagreement table above,
consistency across trials and appraisers is not considered here. All
errors are classified as Type I or Type II. Mixed errors are not
relevant.
![]()
A Type I error occurs when the appraiser assesses a good
part/sample as bad (consistency across trials is not considered
here). "Good" is defined by the user in the Attribute MSA analysis
dialog. See Misclassification Legend for specific definition of
Type
I and Type II Errors.
# Inspected = # Good Parts or Samples * # Trials * # Appraisers
Type I Error % = (Type I Error / # Inspected Good) * 100
A Type II error occurs when a bad part/sample is assessed as
good. See Misclassification Legend for specific definition of
Type I
and Type II Errors.
# Inspected = # Bad Parts or Samples * # Trials * # Appraisers
Type II Error % = (Type II Error / # Inspected Bad) * 100
Effectiveness and Misclassification Summary is a summary table of
all appraisers’ correct rating counts and misclassification counts
compared to the known reference standard values.

Attribute MSA Data is a summary showing the original data in
unstacked format. This makes it easy to visually compare appraiser
results by part. If a reference standard is provided, the cells are
color highlighted as follows: agrees with reference (green); Type I
error (yellow); Type II error (red):
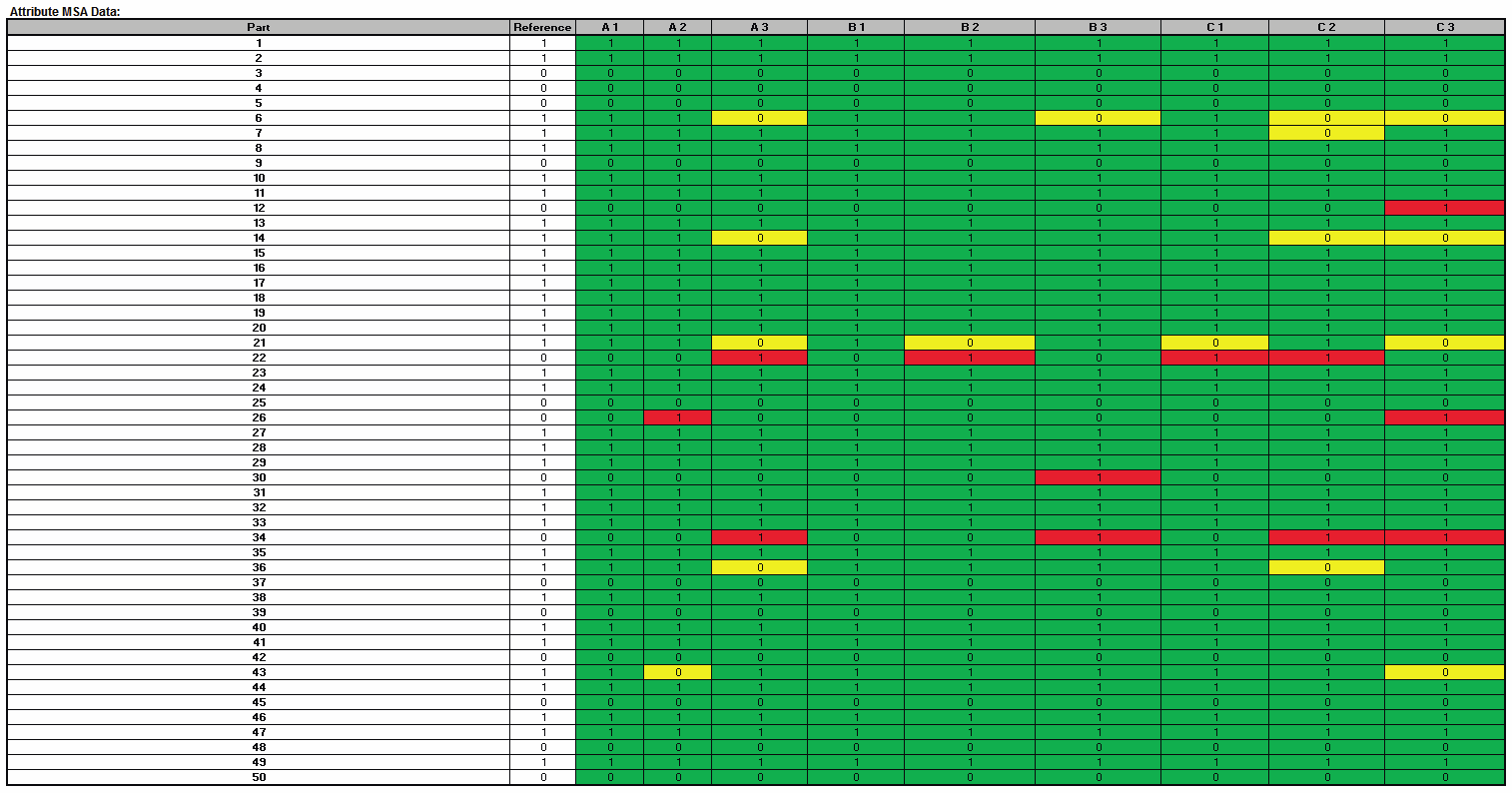
In conclusion, with the Kappa scores in the “yellow zone” (< 0.9) and Percent Effectiveness less than 95% this measurement system is marginal and should be improved. Appraiser B is the exception and does well against the standard. Look for unclear or confusing operational definitions, inadequate training, operator distractions or poor lighting. Consider the use of pictures to clearly define a defect. Use Attribute MSA as a way to “put your stake in the ground” and track the effectiveness of improvements to the measurement system.
Web Demos
Our CTO and Co-Founder, John Noguera, regularly hosts free Web Demos featuring SigmaXL and DiscoverSim
Click here to view some now!
Contact Us
Phone: 1.888.SigmaXL (744.6295)
Support: Support@SigmaXL.com
Sales: Sales@SigmaXL.com
Information: Information@SigmaXL.com